
UNIVERSIT`
A DEGLI STUDI DI PISA
DIPARTIMENTO DI FISICA ‘E. FERMI’
Tesi di Laurea Magistrale in Scienze Fisiche
Curriculum ‘Fisica delle Interazioni Fondamentali’
Ottobre 2013
A GPU-based real time trigger
for rare kaon decays at NA62
Candidato:
Elena Graverini
Relatore:
Prof. Marco Sozzi
Anno Accademico 2012–2013

Contents
Abstract ................................ v
Sommario ............................... vii
Introduction ix
I The NA62 experiment 1
1 The NA62 experiment 3
1.1 Physics objectives ........................ 3
1.2 Theoretical framework ..................... 4
1.3 Previous searches for K+→π+ν¯ν............. 10
1.4 Experimental strategy ..................... 10
2 Experimental setup 15
2.1 Beam .............................. 18
2.1.1 Beam tracking ..................... 20
2.2 Beam detectors ......................... 21
2.2.1 The differential ˇ
Cerenkov counter (CEDAR) ..... 21
2.2.2 The GigaTracker spectrometer ............. 22
2.2.3 The charged anti-counter ............... 23
2.3 Detectors downstream of the decay region .......... 24
2.3.1 A hermetic setup for photon vetoing ......... 24
2.3.2 The STRAW magnetic spectrometer .......... 28
2.3.3 The RICH detector ................... 30
2.3.4 The charged hodoscope ................ 34

iv
2.3.5 The muon veto detectors ................ 34
II A RICH-based online trigger for K+→π+π0rejec-
tion: simulation and design 37
3 An online trigger using the RICH detector 39
3.1 Purpose ............................. 39
3.2 Trigger and Data Acquisition in NA62 ............. 41
3.3 The standard L0 trigger in NA62 ............... 43
3.4 Use of GPUs in triggers ..................... 46
3.5 The K+→π+π0background ................ 47
3.6 Feasibility study ......................... 49
4 RICH reconstruction 51
4.1 Geometric corrections ..................... 53
4.2 Track propagation: upstream magnets ............ 55
4.3 Reconstruction accuracy .................... 58
5 Trigger characterization 63
5.1 βπ−θKπ correlation ..................... 63
5.2 Missing mass .......................... 65
5.3 ˇ
Cerenkov ring radius ...................... 68
5.4 Other possible optimizations .................. 69
5.5 Performance together with the standard L0 trigger ..... 72
III Algorithm development and test 77
6 “Ptolemy”, a two-step algorithm 79
6.1 The necessity for a multi-ring algorithm ........... 79
6.2 Ptolemy’s theorem ....................... 82
6.3 Reparametrization of the photomultipliers lattice ...... 83
6.4 Pattern recognition ....................... 86
6.5 Single-ring fit .......................... 89
7 Implementation on GPUs 93
7.1 GPU architecture and CUDA framework ........... 93
7.1.1 CUDA memory hierarchy ............... 96
7.1.2 Streams and concurrency ............... 96
7.2 Multi-ring algorithm implementation ............. 97
7.2.1 Test framework, data format and input ........ 97

v
7.2.2 Data stream flow and triplet forming ......... 99
7.2.3 Implementation of the kernel ............. 104
7.2.4 Implementation of the trigger ............. 105
8 Tests and conclusions 109
8.1 Trigger efficiency ........................ 109
8.2 Timing tests ........................... 115
8.3 Possible improvements and outlook .............. 119
8.4 Conclusions ........................... 121
Appendix A Ring fitting algorithms 123
A.1 Problem definition ....................... 123
A.1.1 Geometrical parametrisation ............. 124
A.1.2 Algebraic parametrisation ............... 125
A.2 The “math” algorithm ..................... 126
A.2.1 Implementation of the “math” algorithm ....... 127
A.3 The Taubin algorithm ...................... 129
A.3.1 Implementation of the Taubin algorithm ....... 131
Appendix B CUDA code for the Taubin algorithm 135
Appendix C Specifications of the NVIDIA Tesla K20 GPU 139
Bibliography 141
Acknowledgements 147
Abstract
This thesis reports a study for a new real-time trigger for the NA62 experi-
ment based on Graphical Processing Units (GPUs).
The NA62 experiment was devised to study with unprecedented precision
the ultra-rare decay K+→π+ν¯ν, a process mediated by Flavour-Changing
Neutral Currents (FCNC) whose exceptional theoretical cleanliness provides
a unique probe to test the Standard Model. The use of a high-rate kaon
beam will result in an event rate of about 15
MHz
, so high that it will
be impossible to store data on disk without an efficient selection. The
experiment therefore devised three trigger levels, allowing to reduce the
data rate fed to the readout PC farm down to ∼10 kHz.
For this thesis I developed an online trigger algorithm that uses data
fed by the RICH (Ring Imaging CHerenkov counter) detector in real-time
to allow a rejection of the dominant background
K+→π+π0
based on
kinematical constraints.
As a starting point for the development of this algorithm, I verified the
feasibility of such a trigger through Montecarlo simulations. I measured
the reconstruction resolution, achieved by the RICH detector alone, of the
kinematical variables used for the event selection. After that, I analysed the
background rejection power and the signal efficiency of several kinematical
constraints, and I designed an actual trigger algorithm.
The necessity of running the algorithm in real-time, with a maximum
latency of 1
ms
per event, drove the choice of exploiting the parallel com-
puting power of GPUs. A parallelized algorithm was therefore developed,
that can fit up to 4 Cherenkov rings per event. Moreover, a large number of
events are processed concurrently. No parallelized and seedless multi-ring
fitting algorithm existed before.
The developed algorithm consists of a pattern recognition stage, to assign
the hits to up to 4 ring candidates, and of a robust single-ring fit routine.
The program was tested on GPUs, and its performance and execution latency
proved to be compatible with the requirements.
This work proves that alternative trigger designs are possible for the
NA62 experiment, and represents a starting point for the introduction of
flexible GPU-based real-time triggers in High Energy Physics.
Sommario
Questa tesi costituisce uno studio per un algoritmo di trigger in tempo reale
basato su GPU (Graphical Processing Units) per l’esperimento NA62.
NA62 è un esperimento progettato per misurare con precisione il de-
cadimento ultra raro
K+→π+ν¯ν
, un canale mediato da correnti neutre
flavour-changing estremamente sensibile all’eventuale presenza di nuova
fisica. L’elevato rate di eventi rivelati, dell’ordine di 15
MHz
, non permetterà
una archiviazione su disco dei dati non moderata da severi criteri di selezio-
ne. Sono perciò necessari dei livelli di trigger che consentano di ridurre il
rate di eventi salvati fino a circa una decina di kHz.
L’algoritmo sviluppato si basa sull’uso del rivelatore RICH (Ring Imaging
CHerenkov counter). Le informazioni primitive inviate dal RICH vengo-
no valutate in tempo reale, per produrre una decisione di trigger basata
prevalentemente su considerazioni di cinematica.
In una prima fase ho verificato, tramite simulazione Montecarlo, la fatti-
bilità e significatività di tale progetto. Ho dapprima misurato la risoluzione
sulla ricostruzione di alcune quantità cinematiche ricavate utilizzando uni-
camente il rivelatore RICH, poiché per un trigger di primo livello in tempo
reale non sarà possibile mettere in relazione dati forniti da rivelatori diversi.
Ho studiato poi fino a che livello fosse possibile separare il segnale dal fondo,
misurando l’efficienza di reiezione e l’accettanza per il segnale al variare di
alcuni parametri di selezione.
Data la necessità di eseguire il programma in tempo reale, con una laten-
za massima di 1
ms
per evento, si è deciso di sfruttare il potere computazio-
nale parallelo proprio delle GPU (processori grafici ad elevato parallelismo).
E’ stato quindi sviluppato un algoritmo in grado di eseguire simultaneamen-
te non solo le istruzioni relative ad eventi diversi, ma anche i fit di fino a 4
anelli Cherenkov diversi appartenenti allo stesso evento. Nessun algoritmo
parallelo e seedless di questo tipo esisteva in letteratura.
L’algoritmo implementato è composto di due parti: una iniziale di rico-
noscimento di pattern, che estrae il numero di anelli presenti nella matrice
ed identifica gli hit appartenenti a ciascuno di essi, ed una di fit dei singoli
cerchi. Il programma è stato testato su GPU, ed efficienza e tempi di esecu-
zione risultano compatibili con le richieste. Questo lavoro apre la possibilità
di implementare trigger alternativi e flessibili per NA62 e rappresenta un
primo esempio prototipale dell’uso di GPU in tempo reale.

Introduction
This thesis deals with two different aspects of the same project. A prelimi-
nary stage of validation and characterisation was in fact necessary before
starting the development of an actual trigger algorithm. Therefore, this
document is organized in parts. My own work is described in Parts II and III.
Part Ipresents the NA62 experiment, in the contest of which this work
was carried out. Chapter 1outlines the main Physics goal, that is the study
of the ultra-rare decay
K+→π+ν¯ν
. The theoretical framework and Physics
sensitivities of this process are discussed, and a brief report is given about the
previous searches for this decay. Chapter 2focusses on the NA62 detector,
discussing the characteristics of the high-energy beam used to provide kaon
decays, and analyses the purpose and layout of the various sub-detectors.
In Part II I describe the results of my feasibility study, with an evaluation
of the background rejection efficiency of a trigger based on the identifi-
cation of ˇ
Cerenkov rings. Chapter 3describes the trigger chain for the
NA62 experiment, and discusses the benefits of using commercial graphic
processors (GPUs) at the earliest trigger stage. In this chapter I also set
and describe the objectives of my thesis work. In Chapter 4I introduce the
software framework used for all simulations. The reconstruction procedure
I developed to extract physics information from RICH data is discussed in
detail. The outcome of this work is reported in Chapter 5, where I explore
several possible designs for a direct rejection trigger for π+π0events.
Finally, in Part III I describe how I implemented the actual GPU trigger,
and report on its efficiency and timing tests. Chapter 6presents a general
description of the multi-ring algorithm we designed, divided in a pattern
recognition step and a single-ring fit, and reports the preliminary tests I did

xii Introduction
in order to choose the best single-ring fitting algorithm available. In Chap-
ter 7I briefly introduce the CUDA toolkit, and I go through the technical
details of the GPU algorithm, including some pieces of code. Tests of the
program functioning and timing have been performed, whose results are
reported and examined in Chapter 8. There I also sum up the present status
of this work and discuss the conclusions which may be drawn from this
experience.
I thought it useful to devote some pages to the mathematical analysis
of the main single-ring fitting methods I used. Appendix Ais a brief intro-
duction to the problem of circular regression, and describes two different
algebraic algorithms. The code with which I implemented the chosen fit-
ting method in the trigger algorithm is available in Appendix B. Finally,
Appendix Clists useful specifications of the specific graphic card used to
implement and test the trigger.
Part I
The NA62 experiment

1
The NA62 experiment
Contents
1.1 Physics objectives ..................... 3
1.2 Theoretical framework .................. 4
1.3 Previous searches for K+→π+ν¯ν........... 10
1.4 Experimental strategy ................... 10
The NA62 experiment was devised to study the ultra-rare decay
K+→
π+ν¯νat the SPS (Super Proton Synchrotron) at CERN.
This process was first observed at BNL in the dedicated experiments
E787 and E949 (1997-2001), and its branching ratio was later measured to
be
(1.73+1.15
−1.05) 10−10
[9]. The exceptional theoretical cleanliness of this decay
channel makes it extremely attractive to test the Standard Model predictions
and probe the existence of new Physics.
NA62 was designed to collect the higher statistics ever obtained for
K+
decay events, allowing for a 10% measurement of the branching ratio of the
K+→π+ν¯νdecay with a 10:1 signal to background ratio.
1.1 Physics objectives
The decays
K+→π+ν¯ν
and
K0
L→π0ν¯ν
, the latter being studied by the
KOTO experiment in Japan [37], are unique probes to test the Standard
Model.

4 The NA62 experiment
Both decays are Flavour-Changing Neutral-Current (FCNC) processes, a
kind of transition that is strongly suppressed in the Standard Model and
therefore very sensitive to SM extensions or new Physics scenarios, as sum-
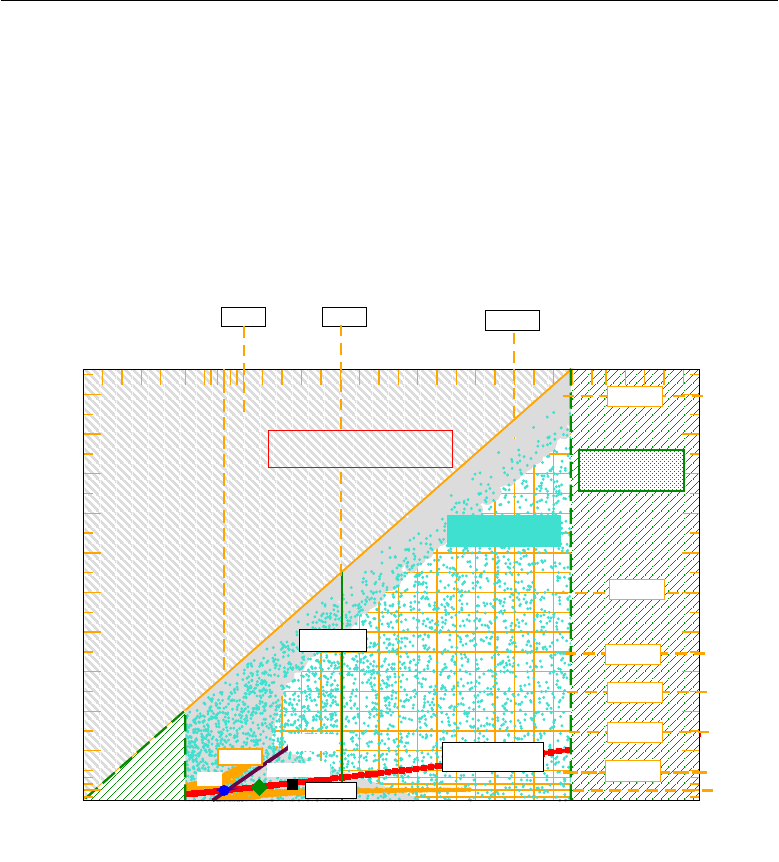
marised in Figure 1.1. This plot reports the branching ratios predicted by the
Standard Model and by BSM (Beyond the Standard Model) theories such
as the Constrained Minimal Flavour Violation effective theory, the Minimal
Supersymmetric Standard Model and the Four-Generation model [28]. A 10%
measurement of
B.R.(K+→π+ν¯ν)
alone would rule out a large set of
models.
Moreover, the above processes feature an exceptional cleanliness and
precise theoretical prediction: in the NA62 case, the Standard Model pre-
diction is B.R.
(K+→π+ν¯ν) = 7.81+0.80
−0.71CKM ±0.2910−11
[16], where the
first error accounts for the uncertainty on the CKM matrix elements, and
the second one is the pure theoretical uncertainty. Any deviation from this
expectation would be an evidence for new Physics. These decay channels
are thus extremely sensitive, and represent a powerful tool to probe theories
beyond the Standard Model (Figure 1.1) [35,46].
Both processes arise from a
s→dν¯ν
transition at quark level, and can
be described by “penguin” Feynman diagrams (1-loop diagrams). If a dis-
crepancy were detected between experimental data and SM predictions,
this would be a hint for the existence of unknown particles intervening in
the loop. We will discuss further in Section 1.2 the theoretical framework
behind this kind of transition.
In case of agreement with the Standard Model, instead, a precise mea-
surement of the branching ratio of this process would improve the accuracy
of the current experimental determination of the
|Vtd|
parameter, which is
one of the least precisely known elements of the CKM matrix. This particular
measurement would be independent from those already obtained in the
analysis of the B system [29,38,59].
1.2 Theoretical framework
In this section the CKM matrix is introduced, whose element
Vtd
we are
going to investigate by measuring the branching ratio of the
K+→π+ν¯ν
process.
1.2 Theoretical framework 5
5.8 8.0 10.2 12.4 14.6 16.8 19.0 21.2 23.4 25.6 27.8
B(K+->π+νν) x 1011
2.9
14.1
25.2
36.4
47.6
58.8
70.0
81.2
92.4
103.6
114.8
B(KL->π0νν) x 1011
BSM
5 x BSM
9 x BSM
13 x BSM
20 x BSM
28 x BSM
36 x BSM
BSM 1.8 x BSM 3.0 x BSM
45 σ
18 σ
3 σ
150 σ
90 σ
600 σ
300 σ
30 σ
Excluded area
Grossman-Nir bound Excl. 68% CL
E787-949 b.
68%CL
Exp. Bound SM
210 σ
MFV-EFT.(+)
CMFV
MFV-EFT.(+)
MFV-MSSM
MSSM-AU
LHT 331-Z`
4-Gen.
Figure 1.1:
The “Mescia-Smith” plot [28] illustrating
K+→π+ν¯ν
and
K0
L→π0ν¯ν
Physics
sensitivities. Experimental data on the branching ratios of these ultra-rare decays would
allow to put SM and BSM theories at a test.

6 The NA62 experiment
The CKM framework provides an extension to the Cabibbo 2x2 matrix,
that encodes how flavour-changing charged currents (
W±
) couple
u, c
and
d, s
quark states [20]. The coupling is described by means of the intermediate
states
d
and
s
obtained from the mass eigenstates
d
and
s
through a rotation
by an angle θC:
d
s=cos θCsin θC
−sin θCcos θCd
s(1.1)
This way, Cabibbo described the quark mixing using a single real parame-
ter
θC
, named the Cabibbo angle. Information from the experiments that
probed quark flavour transitions yielded the result θC13◦.
The Cabibbo-Kobayashi-Maskawa (CKM) theory generalizes the Cabibbo
matrix including also the quark states b, t from the third generation [39]:
d
s
b
=
Vud Vus Vub
Vcd Vcs Vcb
Vtd Vts Vtb
d
s
b
(1.2)
The current status of experimental results about quark-mixing processes
yields the following evaluations [50]:
|Vud|= 0.97425 ±0.00022 |Vus|= 0.2252 ±0.0009 |Vub|= (4.15 ±0.49) 10−3
|Vcd|= 0.230 ±0.011 |Vcs|= 1.006 ±0.023 |Vcb|= (40.9±1.1) 10−3
|Vtd|= (8.4±0.6) 10−3|Vts|= (42.9±2.6) 10−3|Vtb|= 0.89 ±0.07
(1.3)
From the above values, which were obtained by averaging various mea-
surements, it can be inferred that the diagonal elements are clearly do-
minant. The most favoured transitions are indeed those between quarks
belonging to the same family, i.e.
u↔d
,
c↔s
and
t↔b
. Transitions be-
tween quarks from different families are instead suppressed at various levels.
Unlike the Cabibbo matrix, the CKM matrix does not represent a pure
rotation, as it also includes complex parameters. It can be indeed rewritten
in the following form, making use of the Wolfenstein parametrisation [71]:
VCKM =
1−λ2/2λ Aλ3(ρ−iη)
−λ1−λ2/2Aλ2
Aλ3(1 −ρ−iη)−Aλ21
+O(λ4)
(1.4)

1.2 Theoretical framework 7
VudV∗
ub +Vcd V∗
cb +VtdV∗
tb = 0
Im
Re
ρ(1 −λ2/2)
η(1 −λ2/2)
γ
α
β
VtdV∗
tb
VcdV∗
cb
VudV∗
ub
Figure 1.2:
Unitarity triangle defined by the relation
VudV∗
ub +VcdV∗
cb +VtdV∗
tb = 0
in the
complex plane.
where
A, λ > 0(1.5)
λ= sin θ12 = sin θC(1.6)
Aλ2= sin θ23 (1.7)
Aλ3(ρ−iη) = sin θ13e−iϕ (1.8)
In the Wolfenstein parametrisation,
θij
are three real Cabibbo-like angles,
while e−iϕ is a complex phase term encoding CP violation.
Nine conditions arise from the unitarity of the CKM matrix:
i=u,c,t
V∗
ikVij =δjk j, k =d, s, b (1.9)
j=d,s,b
V∗
jkVij =δik i=u, c, t;k=d, s, b (1.10)
The six vanishing combinations can be represented as triangles in the com-
plex plane (as in Figure 1.2).
According to the Standard Model, the
K+→π+ν¯ν
transition is forbid-
den at tree-level, and thus it arises from the one-loop contributions shown
in Figure 1.3.
Separating the contributions of the quarks
u
,
c
and
t
, intervening as
internal lines, at the leading non-trivial order the amplitude of the
s→dν¯ν

8 The NA62 experiment
ν
d
e, µ, τ
W
ν
W
su, c, t
ν
s
ν
Z
u, c, t
W
u, c, t
d
ν
s
ν
Z
u, c, t
W
d
W
Figure 1.3:
A
W−
box and two
Z−
penguin diagrams. These are the one-loop Feynman
diagrams contributing to the s→dν¯νprocess.
process may be expressed as
A(s→dν¯ν) =
q=u,c,t
V∗
q sVqd Aqwith (1.11)
Aq∼m2
q
m2
Wδ
(δ > 0) q=u, c, t (1.12)
The top quark term dominates, due to its higher mass. As a consequence
this process can be well described by short-distance dynamics, with the
effective Hamiltonian [47]
Heff =αGF
2√2πsin2θW
l=e,µ,τ V∗
csVcdXl+V∗
tsVtdΥt(¯sd) (¯νlνl)(1.13)
where
GF
,
α
and
θW
are the Fermi and fine-structure constants and the
Weinberg angle, respectively.
Υt
is a function representing the dominant top
quark contribution, whose associated uncertainty is very small and mainly
due to the experimental error on the top quark mass: [58]
Υt= 1.469 ±0.017 ±0.002 (1.14)
where the two uncertainties correspond to QCD next-to-leading order and
two-loops EW corrections respectively. The
Xl
functions (with
l=e, µ, τ
)
encode instead the charm quark contributions and can be computed at the
next-to-next-to-leading order with an error lower than 4% [36]. Finally, the
terms (¯sd)and (¯νlνl)represent V−Aneutral weak currents.
Since the coupling amplitude depends on the semi-leptonic operator
(¯sd) (¯νlνl)
, the hadronic part of the amplitude of the studied process can
be determined from that of the decay
K+→π0e+νe
by means of isospin

1.2 Theoretical framework 9
symmetry, leading to [17,18]
BR(K+→π+ν¯ν)
BR(K+→π0e+νe)=rK
λ2Im(V∗
tsVtd)2Υ2
t(1.15)
+λ4Re(V∗
csVcd)P0+Re(V∗
tsVtd)Υt2
In this equation, P0describes the total charm quark contribution
P0=1
λ42
3Xe+1
3Xτ= 0.42 ±0.06 (1.16)
under the assumption
Xµ=Xe
[18], and
rK= 0.901
provides the necessary
isospin-breaking corrections to be applied in order to relate
BR(K+→
π+ν¯ν)to BR(K+→π0e+νe).
The theoretical expectation is then
BR(K+→π+ν¯ν) = 7.81+0.80
−0.71 ±0.29·10−11 (1.17)
where the uncertainties were separated in order to highlight the first contri-
bution, which is due to the input CKM parameters [16].
In the Wolfenstein parametrisation introduced above,
Vts −Vcb
at the
leading order, and |Vcb|,|Vcs|and |Vcd |are currently well known. Therefore
we are left with the only free parameter
Vtd
, to be experimentally deter-
mined with an uncertainty theoretically as low as 5 – 7% [16].
Our current knowledge of
|Vtd|
mainly derives from the analysis of the
neutral strange B meson system. The most accurate measurement of the
mass difference
∆ms=m(B0
s)−m(¯
B0
s)
was obtained averaging CDF [2]
and LHCb [1] results, yielding
∆ms= (17.719 ±0.043) ps−1(1.18)
that, through QCD calculations [40], yields to a combined
|Vtd|
/
|Vts|
measurement:
|Vtd|= (8.4±0.6) ·10−3(1.19)
|Vts|= (42.9±2.6) ·10−3(1.20)
|Vtd/Vts|= 0.211 ±0.001 ±0.006 (1.21)
As discussed above, an alternative determination of the
|Vtd|
parameter
is possible through the branching ratio of
K→πν ¯ν
decays. This kind of
processes arising from loop contributions is very sensitive to new Physics,
and can be used to over-constrain the CKM matrix elements and check for
deviations from the Standard Model.

10 The NA62 experiment
1.3 Previous searches for K+→π+ν¯ν
The earliest searches for the
K+→π+ν¯ν
decay date back to 1969, when a
bubble chamber experiment at the Argonne National Laboratory of Michigan
defined a first upper limit to its branching ratio [22]:
BR(K+→π+ν¯ν)<10−4(1969) (1.22)
Four years later, the limit was improved to
BR(K+→π+ν¯ν)<5.6·10−7
by a spark chamber experiment at the Berkeley Bevatron [21], followed by
a search at the KEK Proton Synchrotron that yielded [11]
BR(K+→π+ν¯ν)<1.4·10−7(1981) (1.23)
Since the 80’s, a large effort has been devoted at the Brookhaven National
Laboratory to the study of rare, ultra-rare and forbidden kaon decays.
The E787 collaboration published a first measurement based on 3 events
interpreted as K+→π+ν¯νdecays [7]:
BR(K+→π+ν¯ν) = 1.47+1.30
−0.89 ·10−10 (2004) (1.24)
The follow-up experiment E949 was able to collect 7 more candidate
events with an estimated background of
0.93+0.32
−0.24 ±0.17
events, where
the first error accounts for the experimental systematics and the second
represents the pure statistic uncertainty, leading to a combined result of [9,
10]
BR(K+→π+ν¯ν) = 1.73+1.15
−1.05 ·10−10 (2009) (1.25)
which is consistent with the Standard Model expectations, within the large
statistical errors.
It is important to note that every
K→πν¯ν
experiment performed up to
now has used low-energy stopped-kaon beams. NA62 will instead employ a
high-energy beam, thus studying in-flight kaon decays.
1.4 Experimental strategy
The presence of two neutrinos and of a single charged track in the final
state makes NA62’s goal a challenging precision measurement, requiring
hermetic background rejection as well as an excellent detector system for
particle identification, tracking, calorimetry and spectrometry. The signature

1.4 Experimental strategy 11
Large angle photon vetoes
OPAL lead glass
Forward γveto
NA48 LKr
RICH µ/π ID
1 atm Ne
Dipole spectrometer
4 straw-tracker stations
µveto
Fe/scint
Charged
veto
Beam tracking
Si pixels, 3 stations
Differential ˇ
Cerenkov
for K+ID in beam γveto
γveto
4 m
KTAG CHANTI
LAV RICH MUV
GIGATRACKER
STRAW LKr
IRC
SAC
0 50 100 150 200 250 m
Fiducial volume ∼60m
10−6mbar
5 MHz K+decays
Figure 1.4:
Sketch of the full NA62 detector. The CEDAR (KTAG), 8 out of 12 LAV stations,
the LKr and SAC calorimeters and the CHOD used for NA48 are already installed on site.
The CHANTI, the STRAW spectrometer, the RICH, the IRC calorimeter and the muon vetoes
are currently under construction, while the GTK is in a phase of advanced design [51]. See
Chapter 2for a brief description of the above subdetectors.
of a
K+→π+ν¯ν
decay consists in one and only one charged track. Any
other event for which only one charged track is detected contributes to the
background.
The
K+→π+ν¯ν
process features only three measurable quantities,
which are the momenta of the kaon and of the charged decay product, and
the laboratory frame angle between the two. It is convenient to construct
the squared missing mass to the kaon and the measured decay product, and
use it as a discriminating kinematic variable:
m2
miss = (Pµ
K−Pµ
π)2(1.26)
= (EK−Eπ)2−P2
K+P2
π−2|PK||Pπ|cos θKπ
where
PK
and
Pπ
are the momenta of the decaying kaon and of the pion,
EK
and
Eπ
are their energies and
θKπ
is the decay angle in the laboratory
frame, i.e. the angle between the kaon and pion tracks.
The missing mass is computed under the assumption that the detected
decay product is a pion. The
m2
miss
variable allows to separate the signal
from the most important background processes, as shown in the first panel
of Figure 1.5. The “fiducial” signal region, i.e. the
m2
miss
interval allowed for

12 The NA62 experiment
Decay mode B. R. Rejection
µ+νµ63% Kinematics + µPID
π+π021% Kinematics + γVeto
π+π+π−6% Kinematics + π±Veto
π+π0π02% Kinematics + γVeto
π0e+νe5% ePID + γVeto
π0µ+νµ3% µPID + γVeto
Table 1.1: Main background channels for the NA62 experiment.
data analisys, is split into two parts, excluding the region dominated by the
K+→π+π0
process. In addition, upper and lower limits are set in order to
isolate the
µ+ν
and
3π
channels. These three channels account for 92% of
the K+decay events [50].
The second panel of Figure 1.5 gathers missing mass spectra for back-
ground modes which are not kinematically constrained. These modes
include radiative versions of the channels described above, and
3−
and
4−
body semi-leptonic channels. In these cases, the missing mass distribu-
tions overlap that of the signal; hence the only way to push background
rejection to the needed limits for these processes is to employ reliable parti-
cle identification (PID) and VETO systems.
Table 1.1 lists the most frequent
K+
decay modes, together with the
respective rejection techniques.
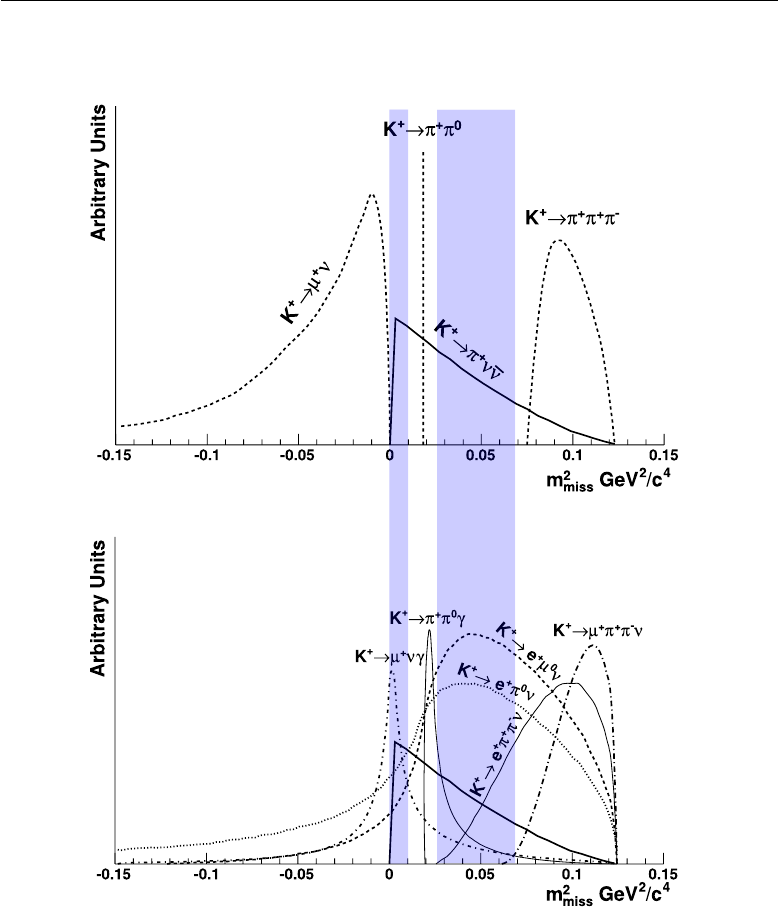
1.4 Experimental strategy 13
Figure 1.5:
Distribution of the recostructed squared missing mass resulting from the decay
of the generated kaon into the detected charged daughter, under the assumption that
the latter is a pion. The solid line represents the
K+→π+ν¯ν
signal in both plots. The
first sketch shows the shape of the kinematically constrained backgrounds, which are also
the channels with the largest branching ratios. The second plot shows the other main
background processes for which the reconstructed missing mass overlaps that of the signal.
The distributions shown here were computed without taking into account the errors due
to the finite resolution of the NA62 detector [23]. The darkened areas display the current
choice for the fiducial signal regions.

2
Experimental setup
Contents
2.1 Beam ............................ 18
2.1.1 Beam tracking .................... 20
2.2 Beam detectors ....................... 21
2.2.1 The differential ˇ
Cerenkov counter (CEDAR) . . . . 21
2.2.2 The GigaTracker spectrometer ............ 22
2.2.3 The charged anti-counter .............. 23
2.3 Detectors downstream of the decay region ....... 24
2.3.1 A hermetic setup for photon vetoing ........ 24
2.3.2 The STRAW magnetic spectrometer ......... 28
2.3.3 The RICH detector .................. 30
2.3.4 The charged hodoscope ............... 34
2.3.5 The muon veto detectors ............... 34
The NA62 experiment is located at the CERN-SPS North area, on the
beam line originally used by the NA48 experiment. The NA62 collaboration
devised a new experimental apparatus on the basis of the NA48 experience
[48].
An unseparated 750
MHz
beam composed by protons, pions and a frac-
tion of 6%
K+
is produced by the collision of a 400
GeV/c
proton beam on
a Beryllium target. The fiducial decay region begins approximately 100
m
downstream of the target, and ends 70
m
farther, where the downstream

16 Experimental setup
Figure 2.1: Schematic view of the NA62 detector.

17
detectors are located.
Three sub-detectors placed upstream of the decay region monitor the
incoming beam conditions. Beam kaons are identified by the CEDAR, a
ˇ
Cerenkov Differential counter with Achromatic Beam focus. The GTK (Gi-
gatracker) subdetector, a beam spectrometer composed by three stations
of silicon micro-pixels, provides a precise measurement of the beam kaons
momentum, direction and time. Finally, the CHANTI (Charged-Anti) scintil-
lator rings that surround the last layer of the GTK veto large-angle charged
particles before they enter the decay region.
Large-angle photon vetoes (L AV) surround the cylindrical walls of the
vacuum chambers that host the decay region. Together with the downstream
electromagnetic calorimeters, they ensure a photon rejection inefficiency
smaller than
10−8
in a 50
mrad
cone around the
z
axis (i.e. the initial
direction of the kaon beam) [32].
Decay vertex, direction of flight and momentum of the charged decay
products are measured by a straw chambers spectrometer (STRAW) and a
RICH, namely Ring Imaging ˇ
Cerenkov detector. The RICH is also used to
provide
π
–
µ
discrimination in the
15 ≤Pz≤35 GeV/c
region, where
Pz
is
the pion/muon momentum along the zaxis.
A segmented scintillation hodoscope (CHOD) provides fast trigger signals
for charged particles just after they emerge from the RICH vessel. Down-
stream, three calorimeters provide small-angle photon veto. The LKr (Liquid
Krypton) detector is an electromagnetic calorimeter which can also provide
a selective
e+
/
e−
trigger by measuring the energy deposit and the shape of
the electromagnetic showers developed in its volume. An intermediate ring-
shaped calorimeter (IRC) and the small-angle electromagnetic calorimeter
(SAC ) add photon suppression in the region not covered by the geometric
acceptance of the LKr. In particular, a dipole magnet is installed in order
to bend charged beam particles away from the
z
axis, so that only forward
photons can hit the SAC.
Suppression of the
K+→µ+νµ
background requires fast and hermetic
muon vetoing. A scintillator system (MUV3) detects muons emerging from
an 80
cm
thick iron block. Two additional muon-veto stations are pro-
vided by the MUV1 and MUV2 calorimeters, used to distinguish muons from
hadrons by measuring the energy released and the shape of the hadronic
showers initiated by the particle that has to be identified.

18 Experimental setup
A longitudinal view of the experimental setup devised by the NA62
collaboration is shown in Figure 2.1. For clarity, I will divide the sub-
detectors into two subsets: the beam detectors, upstream of the decay
region, and the downstream detectors, used to detect and characterize the
decay products.
2.1 Beam
Empirical results achieved in 1980 [12] show that it is convenient to use a
high energy proton beam in order to maximize the production of positive
kaons by beam interaction on a Beryllium target.
The highest kaon production is achieved at
PK/Pp0.35
, where
Pp
is the central proton beam momentum, and
PK
is the momentum of the
produced kaons. In addition, the number of kaons that decay in the fiducial
region reaches its maximum for
PK/Pp0.25
. These quantities increase
with
P2
K
and
PK
, respectively [32]. Furthermore, the use of high energy
kaons increases the detection efficiency of most sub-detectors. Due to these
considerations, it was decided to fix the central beam momentum at 75
GeV/c.
The choice of positive kaons is determined by the following ratios of
particles abundances in a beam produced with 400 GeV/cprotons: [32]
K+/K−2.1(2.1)
K+/π+
K−/π−1.2(2.2)
A fiducial momentum range for the detected pion is defined between
15 and 35
GeV/c
. In fact, in the RICH detector pions from
K+
decay are
well separated from background muons only if their energy is higher than
approximately 15
GeV
(see Section 2.3.3). Moreover, an upper limit to the
energy of accepted pions is set at 35
GeV
, so that other particles originating
from
K+
decays must carry an energy of 40
GeV
, and thus be comfortably
detectable if they are not neutrinos. This way, the detector hermeticity with
respect to the background for the studied decay channel
K+→π+ν¯ν
is also
increased.

2.1 Beam 19
Beam characteristics 60 GeV/c75 GeV/c120 GeV/c
Fluxes at production
p 89 171 550
K+40 53 71
π+353 532 825
total 482 756 1446
Survival factor over 102 m K+0.797 0.834 0.893
π+0.970 0.976 0.985
Fluxes at 102 m from target
p 89 173 550
K+32 45 63
π+343 525 813
total 464 743 1426
Decays in 60m fiducial length K+3.9 4.5 4.1
π+6.1 7.4 7.2
K+decays / π+decays in 60m 0.64 0.61 0.57
K+decays in 60m / total hadr. flux ·10−38.4 6.1 2.9
K→πνν acceptance (R1, no Pπmax) 0.08 0.11 0.11
Acc. K→πνν /1012 proton s−1·106B.R. 0.31 0.50 0.45
Acc. K→πνν /π+decays in m ·B.R. 0.052 0.067 0.062
Acc. K→πνν / total hadr. flux ·10−3B.R. 0.67 0.67 0.31
Table 2.1:
Criteria for the choice of the central beam momentum [32]. Fluxes and decay
rates are expressed in units of
106s−1
and normalized to
1012
incident protons per second.
Fluxes are measured in a solid angle
∆Ω = 42 µsr
, and allow for a momentum spread
∆P/P = 1%.
Table 2.1 summarizes the criteria examined in order to choose the mo-
mentum of the kaon beam.
Let us briefly discuss how the final kaon beam is produced. A focalised
400
GeV/c
proton beam extracted from the SPS is driven onto a 40
cm
thick beryllium target with a diameter of 2
mm
. The emerging beam passes
through a 95
cm
long copper collimator, which absorbs particles propagat-
ing at angles greater than 6
mrad
before they can decay. Three subsequent
quadrupole magnets define a spatial acceptance of 3
mrad
along the hori-
zontal direction (
x
) and 5.2
mrad
along the vertical direction (
y
) around a
central beam momentum of 75
GeV/c
[32]. Two subsequent dipoles select
the positive component of the beam. A 1.06
X0
thick tungsten radiator is
placed in the middle of this 4-dipole achromatic optic element, in order

20 Experimental setup
Momentum 75 ±0.9GeV/c
Rate 750 MHz
Composition
70% π+
23% p+
6% K+
1% other
Table 2.2: Features of the final mixed beam entering the fiducial decay region.
to reduce the positron energy at such a level that the beam optics can
reject positrons up to 99.6%. Finally, two remaining dipoles, and then
three quadrupole magnets, refocus the beam onto its original direction
along the
z−
axis. The whole system ensures a momentum acceptance band
|∆P/P | 1%.
After entering the vacuum chamber, the beam is focused again to an
aperture of 4 mrad by a 1.8 m long collimator with a diameter of 28 mm.
The characteristics of the final beam are shown in Table 2.2.
2.1.1 Beam tracking
In Section 2.2.1 I will describe the CEDAR detector used to tag
K+
in the
beam. The CEDAR is preceded by an adjustable collimator that ensures that
the beam is sufficiently large and parallel to match the detector require-
ments, and by a vertical steering magnet. Two pairs of scintillator counters
in coincidence monitor the divergence of the beam, and their feedback is
used to tune the beam optics in order to suppress the beam divergence.
A system composed by the Gigatracker detector (described in Sec-
tion 2.2.2), four achromatic C-shaped dipoles, and a horizontal steering
magnet is used to track the beam kaons. The achromatic dipole system
deflects the beam in the vertical direction, providing a 60
mm
displacement
that allows to measure the track momentum with a resolution of 0.2%.
Between the second and the third dipole there is a 5
m
long toroidal
collimator, made of magnetized iron, whose aim is to defocus the muon
content of the beam. The “return fields” in the yokes of the following dipoles

2.2 Beam detectors 21
supplement the defocussing action of the collimator. The overall system can
intercept and deflect muons out of the spatial acceptance of the beam for
momenta Pµ<55 GeV/c[32].
Just before the last station of the Gigatracker, a horizontal magnet
deflects the beam by an angle
θK= 1.2mrad
towards the positive side
of the
x
axis. This way, the subsequent deflection of -3.6
mrad
towards
x < 0
that allows the STRAW spectrometer to track the decay products
(see Section 2.3.2) directs the beam back into the central hole of the LKr
calorimeter (Section 2.3.1).
2.2 Beam detectors
2.2.1 The differential ˇ
Cerenkov counter (CEDAR)
One disadvantage of high-energy beams is that kaons cannot be efficiently
separated from the
p/π
content of the beam by means of the beam optics.
As a consequence, upstream detectors are exposed to about 17 times the
“useful” rate of particles. The identification of kaons before they decay is
indeed a critical aspect in such a high-rate environment.
Positive kaon tagging is achieved by letting the beam traverse a differen-
tial ˇ
Cerenkov counter (CEDAR). The detector is filled with hydrogen at a
pressure of 3.6 bar, and it has a total thickness of 6.6 X0.
A particle crossing a radiator with refractive index
n
at a speed
β
emits
a cone of ˇ
Cerenkov light at an angle
θc(β, n)
(see Chapter 2.3.3). Since
the momentum of the beam is known, the ˇ
Cerenkov angle, at a fixed gas
pressure and therefore fixed
n
, is a function of the mass of the particle. The
gas pressure is therefore adjusted so that only the wanted particle type can
emit ˇ
Cerenkov radiation at the chosen light detection angle.
The ˇ
Cerenkov light is reflected by a spherical mirror onto a ring-shaped
diaphragm that vehicles light into 8 clusters of 32 photomultipliers each
[32]. The number of photomultipliers was increased, compared to the origi-
nal CEDAR on the beam line, in order to decrease the photon rates on each
readout device, reducing dead time and accidental noise as a consequence.

22 Experimental setup
Figure 2.2:
On the left, a pressure scan on a 75
GeV
beam shows three peaks, corresponding
to pions, kaons and protons respectively. The plot shows the counting rate of the CEDAR
detector, normalized to the total beam rate, as a function of the pressure of the N
2
gas
filling the chamber [23]. The panel on the right displays the photons for 100 simulated
CEDAR events: ellipsoidal mirrors defocus the light onto the photodetector planes, in order
to lower the counting rate of each photomultiplier [32].
2.2.2 The GigaTracker spectrometer
The name “Gigatracker” derives from the high rate of particles that this
spectrometer must sustain. Due to the non-uniform 750
MHz
beam rate,
the particle flux presents a peak of 1.3
GHz/mm2
around the centre of the
detector.
The Gigatracker provides precise measurements of the angle, momentum
and time of the crossing particle. The resolutions to be achieved are:
time 150 ps
momentum ∆p / p ≤0.2%
direction 16 µrad
Such accurate measurements are necessary in order to correctly associate
the decaying kaon with the
π+
track detected downstream. Kinematic
selection of
K+→π+ν¯ν
events indeed relies on constraints based on the
missing mass variable, defined as
m2
miss ≡(PK−Pπ)2
m2
K1−Pπ
PK+m2
π1−PK
Pπ−PKPπθ2
Kπ (2.3)
2.2 Beam detectors 23
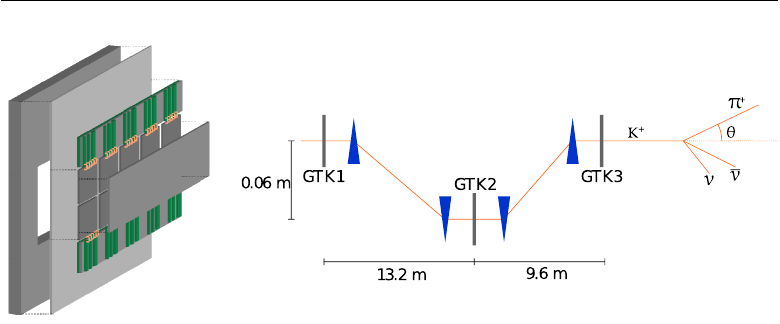
Figure 2.3:
On the left, sketch of a Gigatracker station [23]. On the right, layout of the
Gigatracker stations and magnets used to bend the beam [68].
In this equation,
PK
entirely derives from the Gigatracker data, and the de-
termination of
θKπ
makes use of both the GTK and the downstream STRAW
spectrometer.
In order to limit hadronic interactions and to preserve the beam diver-
gence, the Gigatracker is composed of three stations for a total thickness
lower than 0.5 X0[32]. Each station contains 18000 300×300 µm2silicon
micro-pixels 200
µm
thick bump-bonded to 10 readout ASIC chips 100
µm
thick. A sketch of a Gigatracker station is shown in Figure 2.3(a).
The three stations of the GTK are mounted inside the vacuum tank pre-
ceding the decay region, and they are interlaced with 4 achromat magnets
as shown in Figure 2.3(b).
An extensive amount of resources was committed to the design and
development of this detector. Critical aspects are the high radiation hardness
needed to sustain the rate of beam particles crossing the silicon sensors,
and the very high time resolution required. In particular, the dissipation of
the increasing leakage current due to radiation damage needs a complex
cooling system. This will be based on a micro-channel cooling system.
2.2.3 The charged anti-counter
A vital requirement of the experiment is the reduction of accidental back-
ground to a level of
10−11
. The purpose of the CHANTI (Charged Anti-
counter) is to tag particles propagating at angles larger than that allowed
for the beam as they emerge from the last station of the Gigatracker. Such
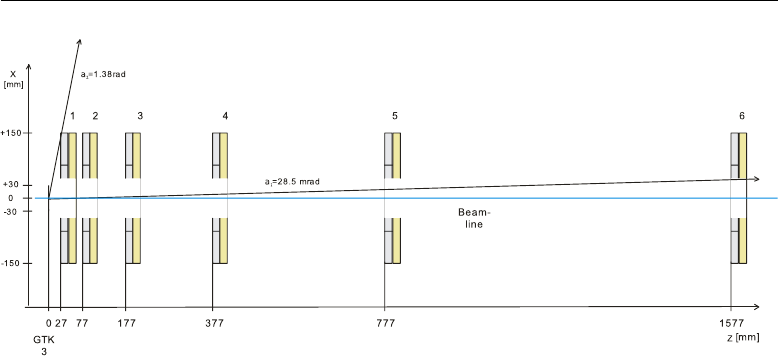
24 Experimental setup
Figure 2.4: Sketch of the six CHANTI stations on the beam line [32].
particles can be produced by inelastic interaction of the beam with the
collimator and upstream material.
A set of large angle guard counters is therefore installed immediately
after the Gigatracker (see Figure 2.4). Further stations, sensitive in the
closest region to the beam, can veto the beam halo muons.
The CHANTI is made of six double-layer stations [32]. Each station is a
30
×
30
cm2
square with a 90
×
50
mm2
rectangular hole to allow the passage
of the beam. Each layer is composed of 24 (22) scintillator bars aligned
to the
x
axis (
y
axis). Light is collected by wavelength-shifting fibers, and
transported to one side of the station, where a silicon photomultiplier is
placed.
2.3 Detectors downstream of the decay region
The downstream detector has been designed to detect
K+
decay products.
Therefore, central beam holes have been arranged in all sub-detectors.
2.3.1 A hermetic setup for photon vetoing
Photons originating from one of the major backgrounds,
K+→π+π0
(
B.R. = 20.7%
), propagate at angles greater than 50
mrad
only in a 0.2%
fraction of
π+π0
events. A photon veto system was therefore developed, that
ensures a rejection inefficiency lower than
10−8
in the fiducial energy range

2.3 Detectors downstream of the decay region 25
of the signal. Photon veto detectors cover a 50
mrad
angular region around
the beam.
The photon veto system is partitioned in four sub-detectors that cover
different angular regions and employ three different technologies:
•
Twelve LAV stations cover the angular region between 8.5 and 50
mrad.
•
SAC and IRC cover the inner angular region, from about 0 to 1
mrad
.
•The LKr calorimeter covers angles between 1 and 8.5 mrad.
The
Large Angle Veto
(LAV) detector reuses the 10
×
10
×
37
cm3
lead-
glass blocks from the OPAL electromagnetic calorimeter [3], arranged in 12
annular stations (Figure 2.5(a)).
Of the 12 LAV counters, 11 are placed inside the
3×10−7mbar
vacuum
tank hosting the decay region, and one is placed between the RICH and the
CHOD sub-detectors.
Each ring-shaped station of the LAV has an increasing diameter as the
distance from the target grows, and consists of four to five rings of lead-glass
blocks read out at the outer side by 76
mm
diameter Hamamatsu photomul-
tipliers.
Photons incident onto the LAV blocks start electromagnetic avalanches,
detected through the collection of ˇ
Cerenkov light emitted by e+e−pairs.
Thanks to its low threshold, the LAV system will be also able to detect
muons and pions in the beam halo [49].
The
Liquid Krypton Calorimeter
(LKr), placed between the RICH and
the MUV detectors, is the same used in the NA48 experiment. Its main
purpose is to reject photons that fly at an angle between 1 and 8.5
mrad
to
a level of
10−5
. However, the LKr can also provide accurate measurements
of the energy of electrons and positrons, useful for the rejection of the
K+→π0e+νebackground.
The calorimeter volume is filled with 9
m3
of liquid krypton, whose
characteristics are summarised in Table 2.3.
In this quasi-homogeneous calorimeter, the active material is 127
cm
(approximately 27
X0
) thick, and can fully contain 50
GeV
showers. The

26 Experimental setup
X04.7 cm
Moliere radius 6.1 cm
Bath temperature 119.8 K
Table 2.3: Characteristics of the liquid krypton filling the calorimeter [67].
active volume is divided in 13248 2
×
2
×
127
cm3
double ionization cells with
Cu-Be ribbons as central anodes (Figure 2.5(b)). Despite being originally
built for the NA48 experiment, the LKr calorimeter is still a state-of-the-art
piece of hardware, featuring excellent resolution in energy, space and time:
σE
E=0.032
√E⊕0.09
E⊕0.0042 GeV (2.4)
σx=σy=0.42
√E⊕0.06 cm (2.5)
σt=2.5
√Ens (2.6)
In the above formulas all energies are expressed in GeV.
Both the small-angle veto calorimeters,
IRC
and
SAC
, are “shashlyk” type
calorimeters, i.e. detectors made of lead absorber layers interspaced with
plastic scintillator plates used as active material [13].
Due to the geometry of the experiment, photons hitting IRC or SAC will
have an energy greater than 5
GeV
. Interacting with the lead plates, they
will then start electromagnetic showers. A wavelength-shifting dopage is
added to the scintillator tiles in order to gather the light emerging from the
showers into fibers read out by photomultipliers.
The
Ring-shaped Calorimeter
IRC is placed around the beam line in
front of the LKr, and covers the angular region between such detector and
the SAC.
A dipole magnet bends the beam so that charged particles cannot hit the
SAC (
Small Angle Calorimeter
), the most forward detector in the NA62
setup.
The combined detection inefficiency of the small angle vetoes is re-
quested to be lower than 10−8.

2.3 Detectors downstream of the decay region 27
(a) A view of the LAV-12 station.
CuBe ribbons Beam tube
Back plate
Front plate
Outer rods
Spacer plates
(b) Liquid krypton calorimeter electrode structure [67].
Figure 2.5:
Technical designs of a LAV station (top panel) and of the LKr calorimeter
(bottom panel).

28 Experimental setup
2.3.2 The STRAW magnetic spectrometer
The purpose of the magnetic spectrometer is to determine the directions and
momenta of secondary particles originating from primary kaon decays. The
kinematical constraints needed to reject most of the background require an
accurate reconstruction of the track of the daughter charged particle. In
particular, in order to achieve proper reconstruction, the needed resolutions
are:
•decay angle: ∆θKπ ≤60 mrad
•momentum: ∆p/p ≤1%
•
spatial resolution:
σx,y ≤130 µm
, in order to correctly trace back the
decay vertex.
In addition to this, a number of experimental requirements need to be
fulfilled. The tracker will be in fact integrated inside the vacuum chamber,
and it needs to minimize the amount of material traversed by the particles
as much as possible. The detector must also be able to operate in a high rate
environment, with a particle flux close to 40
MHz cm−1
in the central area.
The spectrometer is based on the straw technology, its building blocks
being ultra-light straw tubes 2.1
m
long and 9.8
mm
in diameter [32]. The
material employed consists of 36
µm
thin PET foils coated on the inner side
with 50
nm
of copper and 20
nm
of aluminium, acting as cathode; the anode
is a gold-plated tungsten wire, 30
µm
in diameter, placed at the centre of
the tube.
A simulation performed with Garfield
1
has allowed to compare the best
working points for two different gas mixtures: a slower, but more “ageing-
safe” isobutane mixture (CO
2
90% iso-C
4
H
10
5% CF
4
5%), and a faster Ar
70% CO
2
30% mixture. Considerations about the possibility of pile-up of
hits corresponding to different events have led to the choice of the faster
gas mixture.
The full spectrometer consists of four chambers. A dipole magnet, placed
between the second and the third chamber, generates a vertical field of
0.36
T
, corresponding to a kick of 270
MeV/c
directed towards the
x−
axis.
Each chamber is composed of four complementary “views” (
x
,
y
,
u
and
v
), allowing for a redundance of 100%. Each view, finally, is made of 256
straw tubes. Figure 2.6 shows the layout of the views composing a STRAW
1

30 Experimental setup
Figure 2.7:
Details of: the straws for the downstream spectrometer, the CEDAR-KTAG
photomultiplier housing frame, the ribbons defining the cells of the LKr calorimeter [51].
chamber, while a detailed view of the tubes composing a plane is visible in
the first panel of Figure 2.7.
2.3.3 The RICH detector
The main background
K+→µ+νµ
should be suppressed by a factor
10−13
in order to achieve a signal-to-background ratio of the order of 10% for
the
K+→π+ν¯ν
decay [8]. This task will be fulfilled by a combination of
kinematic cuts and direct muon rejection at trigger level.
The
Ring Imaging ˇ
Cerenkov
(RICH) sub-detector in the NA62 setup will
be able to separate pions from muons in the momentum range comprised
between 15 and 35
GeV/c
up to a level of
5×10−3
; moreover, it will also
provide a level 0 trigger primitive for charged tracks. Since this detector is
central to the work described in this thesis, it is here discussed in more detail.
Let us describe the functioning of a RICH detector in general terms,
before discussing the one devised for the NA62 setup.
2.3 Detectors downstream of the decay region 31
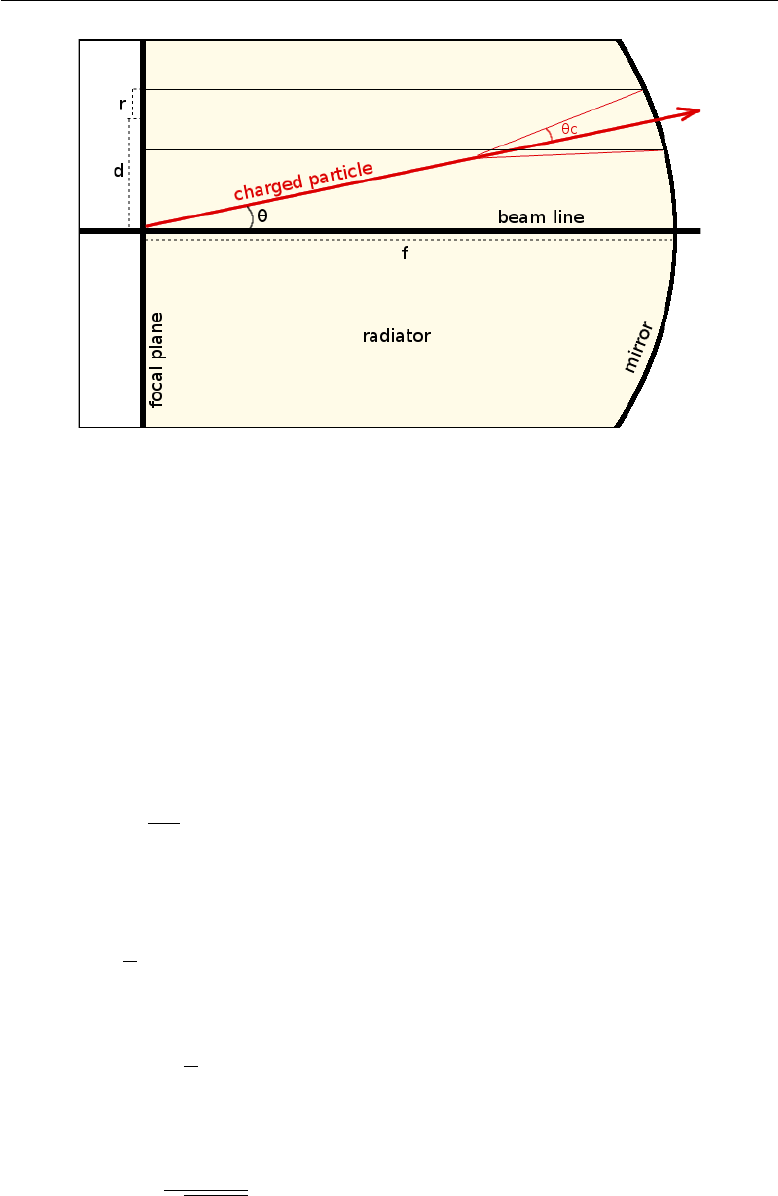
Figure 2.8:
Draft of a simple RICH detector. The radius of the circle in the focal plane is
determined by the velocity of the particle, while the position of its centre depends on the
particle direction.
Principles of a RICH detector
Figure 2.8 describes how a RICH detector works. When a particle goes
through a medium at a velocity
β=v/c > 1/n
, where
n
is the refractive
index of the medium, it emits ˇ
Cerenkov light at an angle
θc
relative to the
particle trajectory, such that
cos θc=1
n β (2.7)
thus forming what is called a ˇ
Cerenkov cone. It follows that a threshold
βth
exists below which no radiation is emitted:
βth =1
n(θc= 0) (2.8)
while the maximum angle of emission is achieved for β→1:
cos θmax →1
n(β→1) (2.9)
From Eqn. 2.8 we derive the threshold momentum
Pth
for a particle of
mass mto emit ˇ
Cerenkov radiation:
Pth(m) = m
√n2−1(2.10)

32 Experimental setup
The light cone is projected on a focal plane, perpendicular to the beam
direction, by means of a spherical mirror (or a system of mirrors, as it will be
described in the following section) of focal length
f
. For particles travelling
parallel to the beam line, the resulting image on the focal plane is a ring of
radius
rc=ftan θc(2.11)
while, for particles travelling at an angle
θ
to the beam line, the same image
appears shifted by a distance
d=ftan θ(2.12)
from the focus. Figure 2.8 shows a sketch of a basic RICH detector.
Larger rings on the focal plane correspond to particles crossing the RICH
radiator volume at a larger velocity (keeping the type of the particle fixed).
On the other hand, if the momentum of the beam is known to an adequate
precision, the radius of the reflected ˇ
Cerenkov ring can be used to compute
the mass of the crossing particle, and therefore to perform P.ID. (Particle
Identification).
The following relation holds:
P(θc) = m
n
1
sin2θmax −sin2θc
(2.13)
and therefore:
P(rc) = mf2+r2
c
r2
max −r2
cm f
r2
max −r2
c
(2.14)
where rmax =f√n2−1.
The NA62 RICH detector
The momentum range and the position of the ˇ
Cerenkov threshold deter-
mined the choice of the gas and gas pressure: the vessel, a 18
m
long and
2.8
m
wide cylinder, will be filled with neon at atmospheric pressure. This
way, the ˇ
Cerenkov threshold momentum for a pion will be
Pth 12.5GeV/c
,
20% smaller than the lower limit of the accepted momentum range. The
refraction index
n
will be such that
(n−1) 60 ×10−6
[32]: according to
Eqn. 2.10, this value almost perfectly corresponds to the emission threshold
2.3 Detectors downstream of the decay region 33
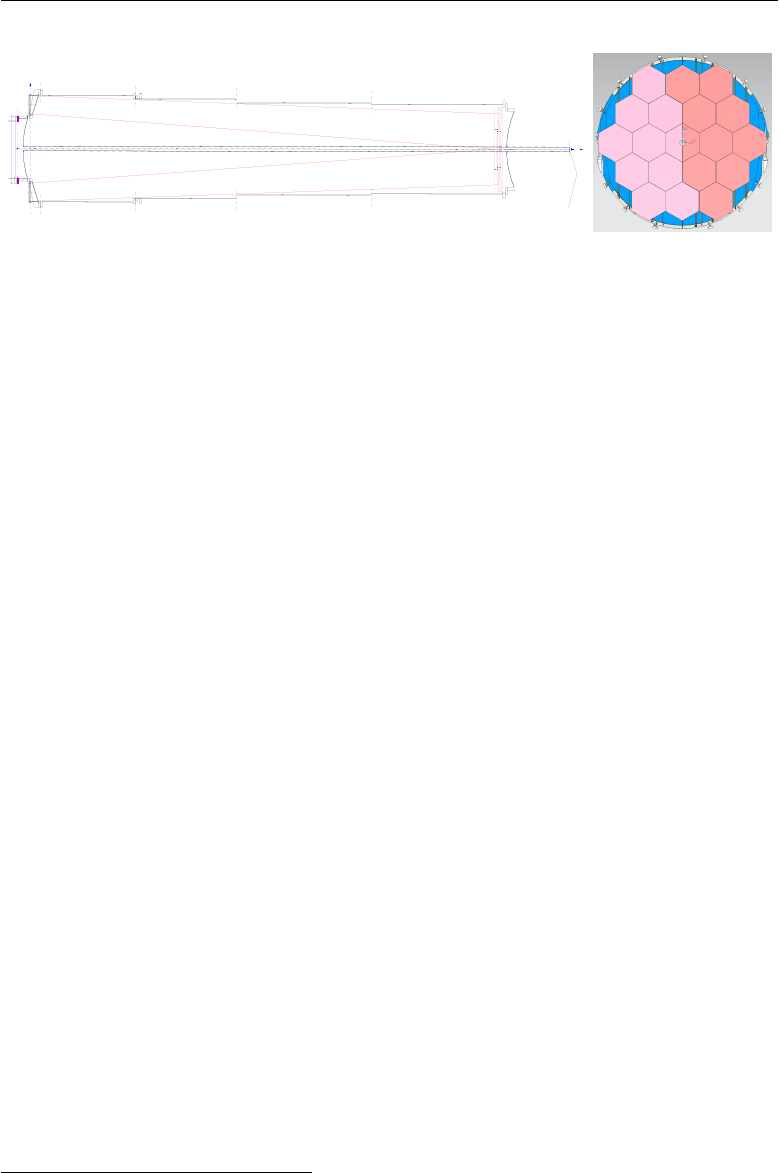
x’
RICH rotated about global y : −1.78085391752183mrad
NOT VALID FOR EXECUTION
Salève
STRAW4
assumed inner diameter of downstream STRAW flange : 2100mm
eccentric−machined interface ring
NA62 RICH : integration parameters 06_Feb_2012
Jura
z
pivot : z’=19727
pivot : z=239600
rotation pivot
36 z=219385
we need "flesh" in the STRAW flange up to diam. 2470mm (otherwise part of fixation bolts would land in vacuum and other part in air)
(a) (b)
Figure 2.9:
Panel 2.9(a): technical drawing of the RICH vessel (the beam goes from right
to left). Panel 2.9(b): front view of the system of 18 hexagonal and 2 semi-hexagonal
mirrors.
for the mass of the charged pion. The Ne gas also guarantees small disper-
sion [8]. Figure 2.9(a) shows the technical design of the vessel that will host
the RICH detector.
The vessel will be placed between the last STRAW chamber and the LKr
calorimeter. It will be rotated by 2.4
mrad
with respect to the
z−
axis: this
way, its central hole around the beam pipe will gather the charged beam
component (and the beam halo) bent by the spectrometer magnet, while
most of the kaon decay products will cross the active volume.
A mosaic of 18 hexagonal and 2 semi-hexagonal mirrors made of alu-
minium-coated 25
mm
thick glass covered with a thin dielectric film, with
sides 35
cm
long, reflects the ˇ
Cerenkov cone onto the RICH focal plane. In
order to avoid absorption of light by the beam pipe, the mirrors actually
form two independent spherical surfaces (shown in Figure 2.9(b)), with
the foci corresponding respectively to the two PMT flanges
2
. The collective
34
m
curvature radius of the mirrors layout results in a nominal focal length
f= 17 m.
Detector simulations showed that the best compromise between the
requirements of photon acceptance and angular resolution, and the need to
maintain the cost of the apparatus at an affordable level, can be achieved
by arranging 1952 photomultipliers on the vertices of the cells of a compact
hexagonal lattice. The layout will consist of two support flanges, 70
cm
in
diameter, each hosting 976 Hamamatsu photomultipliers [32].
2
In the following, the left and right sides will be often referred to as Jura and Salève
flanges respectively, after the two mountains overlooking the Geneva area.

34 Experimental setup
Since the RICH will also participate to the level 0 trigger, producing a
primitive each time a charged particle crosses its volume, a time resolution
of about 100
ps
is required, leading to the choice of fast single-anode photo-
multipliers.
The RICH performance has been tested and verified with particle beams
using a full length prototype [8].
2.3.4 The charged hodoscope
A scintillator hodoscope (CHOD) will provide a fast signal to trigger data
acquisition on the passage of a charged particle. In addition, CHOD in-
formation will be combined with data from the RICH in order to provide
primitives useful for the selection of
π+
tracks at subsequent trigger stages.
Due to its excellent time resolution (
σt200 ps
), this detector will also be a
useful tool during the offline analysis, allowing to match the detected track
with that of the decaying kaon.
Initially, in 2014, the hodoscope will be a refurbished version of the
detector used by the preceding NA48 experiment, to be later replaced with
a new detector. The existing NA48 CHOD consists of two planes of 64+64
plastic scintillator tiles aligned respectively to the
x
and
y
directions. The
scintillation light from the counters is collected by Photonis photomultipliers
via short Plexyglas light guides. The “NEWCHOD” is currently in design
phase. The proposed detector should be built with scintillator tiles of
variable dimension according to the distance from the beam, so that the
particle rate is below 500
kHz
in each counter. Light would be read out
via sets of wavelength-shifting fibres positioned in order to maximise the
detection efficiency [44].
2.3.5 The muon veto detectors
In addition to what achieved with the RICH detector, further muon suppres-
sion is needed up to a level of
10−5
. A calorimetric
muon veto
system will
fulfill this requirement in two steps [32]:
1.
A fast muon veto detector (
MUV3
), with time resolution
σt≤1ns
,
will reject events featuring coincident signals in the GTK and CEDAR
detectors. This will lead to a pions to muons ratio of about 20 already
at the first trigger level.
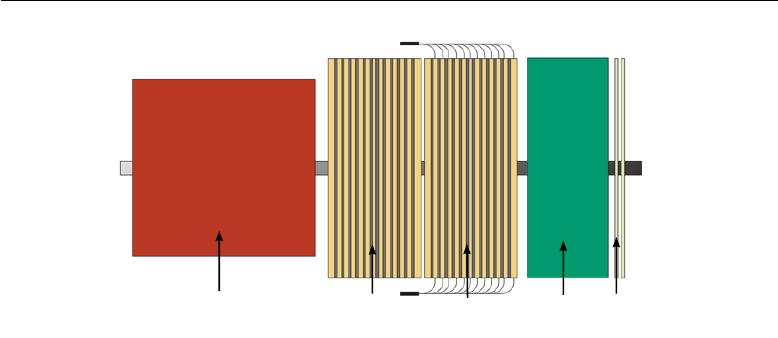
2.3 Detectors downstream of the decay region 35
LKr calorimeter MUV1 MUV2 Iron MUV3
Figure 2.10: Layout of the three MUV detectors.
2.
Two segmented calorimeters (
MUV1
and
MUV2
) will require cross-
ing particles to deposit a significant amount of energy. In addition,
measurements of the shower shape will allow to distinguish those
muons undergoing catastrophic Bremsstrahlung or direct pair produc-
tion from hadrons.
The first two modules, placed around the beam line next to the LKr
calorimeter, are composed of alternate layers of scintillator (10
mm
thick)
and iron (25
mm
thick). The total thickness of each module is 62.5
cm
. The
scintillator bars, 130
cm
long and 4 to 6
cm
wide, are alternatively oriented
along the vertical and horizontal directions.
The third module is placed downstream of an 80
cm
thick iron wall,
and serves as fast level 0 trigger. It consists of a matrix of 20
×
20
×
5
cm3
scintillator blocks read out by photomultipliers.
Figure 2.10 sketches the layout of the three muon veto stations.
Part II
A RICH-based online trigger for
K+→π+π0rejection:
simulation and design

3
An online trigger using the RICH detector
Contents
3.1 Purpose ........................... 39
3.2 Trigger and Data Acquisition in NA62 .......... 41
3.3 The standard L0 trigger in NA62 ............. 43
3.4 Use of GPUs in triggers .................. 46
3.5 The K+→π+π0background .............. 47
3.6 Feasibility study ...................... 49
3.1 Purpose
NA62 was designed to collect approximately
100 K+→π+ν¯ν
events in two
years of data taking. This exceptional statistics will make it possible to probe
this ultra-rare K+decay channel with unprecedented precision.
Accounting for an acceptance of signal events between 10% and 20%,
the experiment was planned in order to allow about
1013 K+
decays in the
fiducial region. With an unseparated
∼
800
MHz
hadron beam containing
approximately 6% kaons, the output event rate of the detectors will be of
the order of magnitude of 10 MHz.
However, a 10
MHz
input rate is unsustainable for any reasonable-sized
offline data acquisition system. A multi-level trigger system was therefore
devised, with the purpose of scaling the data-saving rate down to few tens

40 An online trigger using the RICH detector
of
kHz
. The following list describes the trigger chain to be used in the NA62
experiment:
L0:
hardware synchronous level. Data rate reduction from 10
MHz
to
1
MHz
, with a maximum latency of 1
ms
, using a few fast detectors
only.
L1:
simplified reconstruction of single detectors. Data rate reduction
from 1 MHz to about 100 kHz.
L2:
complete information, full reconstruction. Data rate reduction from
about 100 kHz to about 15 kHz.
The L0 is a fast hardware system that collects information from a few
detectors and uses it to perform a fast event rejection before readout from
the temporary data buffers to the online PC farm. At this stage, simple
assumptions may be done in order to discard a set of data clearly due to
background processes, such as events with more than one charged track,
or featuring signals on any chamber of the muon veto system. Chapter 3.3
describes how the L0 trigger signal is produced.
The maximum latency of the level 0 trigger, i.e. the available time for the
first “decision making” process, was preliminarily set at 1
ms
, a remarkably
large value compared to other High Energy Physics experiments. In princi-
ple, this latency is large enough to allow for deeper analysis on separately
read detectors.
The RICH detector was described in Chapter 2.3.3. Thanks to its fast
response, it will be used in the L0 trigger by providing a multiplicity count.
Much more information is however available from the RICH. The features
of the rings generated by charged particles crossing the RICH volume would
provide the direction and the velocity of the particle as independent mea-
surements. Evaluating this information at the online trigger stage would
allow an important reduction of the event flow. However, since the read-
out system of the RICH detector consists in a matrix of photomultipliers,
information about the particle is available only after a first stage of ring
identification. This identification would also need to be performed online,
which requires very high-speed processing units.
Recent years witnessed the development of a new trend in Information
Technology, i.e. “General Purpose computing on Graphics Processing Units”
(
GPGPU
). Despite being originally designed for 3D computer graphics, mod-
ern commercial GPUs are often exploited to efficiently perform scientific

3.2 Trigger and Data Acquisition in NA62 41
Sub-detector Stations Channels
per station Tot. channels Hit rate
(MHz)
Raw data
rate (GB/s)
CEDAR 1 240 240 50 0.3
GTK 3 18000 54000 2700 2.25
LAV 12 320–512 4992 11 0.3
CHANTI 1 276 276 2 0.04
STRAW 4 1792 7168 240 2.4
RICH 1 1912 1912 11 0.09
CHOD 1 128 128 12 0.1
IRC 1 20 20 4.2 0.04
LKr 1 13248 13248 40 22
MUV 3 176–256 432 30 0.6
SAC 1 4 4 2.3 0.02
Table 3.1:
Payload rates for the 12 sub-detectors of the NA62 experiment. These esti-
mations date back to 2010 [32], and some detectors have been slightly revisited since
then.
computations. Recently, major vendors such as Nvidia and ATI began to
sell processing units and API (Application Programming Interface) libraries
specially designed for this purpose.
In particular, today the computing power and parallel structure of GPUs
seems capable to meet the timing requirements of a low level trigger for
High Energy Physics experiments. The idea at the basis of this Master’s
thesis is to exploit the computing capability of GPUs in order to analyse
the extra track information provided by the RICH detector at the L0 trigger
stage.
3.2 Trigger and Data Acquisition in NA62
The high rate of events and the presence of 12 sub-detectors, for a total
of about 90000 readout channels, results in such a high output data rate
that it is impossible to save them on disk without some type of filtering.
Table 3.1 summarizes the typical payload rates for the primary sub-detectors.
Atrigger system is therefore needed, which should identify the events to be
saved and reject the rest.
The NA62 experiment will feature a unified Trigger and Data Acquisition
(TDAQ) system. Trigger information will be assembled from readout-ready
digitized data, simplifying the subsequent acquisition process [32]. Each

42 An online trigger using the RICH detector
sub-detector readout system will be able to run individually, driven by a
common 40
MHz
clock generated by a single high-stability oscillator and
distributed through optical fibres by the Timing Trigger and Control (TTC)
system designed for the LHC
1
. The building block of the TDAQ system will
be a common general-purpose integrated trigger and data acquisition board
developed in Pisa, nicknamed TEL62 (Trigger ELectronics for NA62) [5].
The TEL62 board is an upgraded version of the TELL1 board used by the
LHCb experiment at CERN [31]. The mechanical and electrical architecture
has been maintained for compatibility, but the new board hosts more pow-
erful FPGAs
2
and a large amount of DDR2 memory, whose size determines
the maximum latency of the trigger process. In fact, four Altera Stratix-III
pre-processing FPGAs (PP) are connected to dedicated TDC
3
boards and to
2
GB
circular memory buffers, where data is stored during real-time evalua-
tion. A central FPGA of the same type, named SyncLink (SL), is connected
to the PPs and to an output mezzanine through high-speed buses. The SL
links data and trigger primitives from all the PPs, stores data in Multi-Event
Packets (MEP), and finally sends them to the output board [5].
Four high performance TDCs are mounted on custom TDCB boards
specifically developed for this application. TDCBs (Time to Digital Con-
verter Boards) are able to service 128 sub-detector channels with a time
resolution of 100
ps
. Four such boards can be plugged on a TEL62, for
a total of 512 channels [25]. The output mezzanine, named Quad-GbE,
is the same equipped by the original TELL1 board, and hosts four 1
Gbit
Ethernet links that can be used to connect the TEL62 board to the central
L0 Trigger Processor (L0TP) or to each other in a daisy-chain configuration.
Several trigger primitives can be packed together into Multi-Trigger Packets
(MTP), allowing a custom number of separate event primitives from the
same detector to be transmitted to the L0TP at the same time, optimizing
the bandwidth usage.
A hardware real time trigger, labelled L0, will command sub-detectors to
transfer data through TEL62 boards to a PC farm through Gigabit Ethernet
links, where data will be stored upon satisfaction of various criteria orga-
nized in levels of increasing complexity and sequentially controlled. Data
are stored in UDP
4
packets for all Ethernet communications, because the
1
2Field Programmable Gate Arrays.
3Time to Digital Converter
4User Datagram Protocol
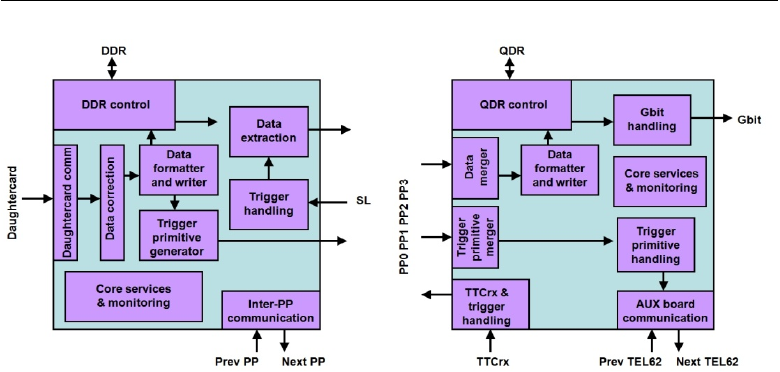
3.3 The standard L0 trigger in NA62 43
Figure 3.1: L0 trigger primitive production: PP and SL firmware block diagrams [5].
simple transmission model of this protocol allows to avoid data processing
overhead at the network interface level. Moreover, the UDP header consists
of only 8
B
of information, and therefore allows for a large payload. A
detailed description of the L0 trigger will be given in Section 3.3.
The software-based trigger hierarchy is organized in two levels, labelled
L1 and L2 respectively, performed on raw data stored on a dedicated PC
farm:
L1
Trigger decisions are taken independently, based on each complete sub-
detector system; however, it is possible to perform logical operations
on the outputs of different sub-detectors.
L2
Trigger decisions are taken on partially reconstructed events, based on
pieces of information assembled from different sub-detectors.
3.3 The standard L0 trigger in NA62
The existing online trigger is hardware-implemented. Data are locally evalu-
ated by each sub-detector involved. Each time a local trigger condition is
satisfied, the sub-detector feeds a timestamped information into a central L0
processor. The latter matches such trigger primitives among all the detectors
involved in the formation of the L0 trigger signal; it then broadcasts back
a timestamped acquisition signal to the sub-detectors when the whole set
of L0 requirements is satisfied. Triggered by this signal, the local front-end
systems feed the corresponding data to the TDAQ PC farm.

44 An online trigger using the RICH detector
The TEL62 firmware is sketched in Figure 3.1. At the online TDAQ level,
the data flow is organized as follows:
1. Detector hits are digitized on the TDCB mezzanines.
2. The PPs receive data from TDCBs.
3.
Part of the data is calibrated and analysed to generate L0 trigger
primitives (this process is different for each sub-detector). Event data
is stored into circular memory buffers.
4.
The trigger primitives from all the PPs are collected by the SL, and
merged if their time windows overlap.
5. A timestamped trigger primitive is assembled on the SL.
6.
A number of trigger primitives is stored. When the predefined MTP
size is reached, the Multi-Trigger packet is sent to the L0TP through a
dedicated Ethernet link.
7.
The L0TP matches the primitives from all the L0 trigger sources, and
decides if a timestamped L0 trigger signal should be communicated to
all the TEL62s.
8.
Upon receiving a trigger signal, the SL commands the PPs to fetch data
associated to the corresponding timestamp from the memory buffers.
9.
Triggered event data are assembled on the SL until the predefined
MEP size is reached.
10.
A Multi-Event packet is assembled, and sent to the L1 PC farm through
Ethernet links.
A L0 trigger based on a few simple, uncorrelated conditions is set up
in order to quickly reduce data rates [62]. The sub-detectors responsible
for the L0 trigger need to provide identification of charged tracks (
CHOD
/RICH), and vetoing of the most important backgrounds (LKr calorimeter
for 2πand 3πevents, and MUV for muons).
The following conditions were therefore devised to perform a first selec-
tion of πν¯νevents over background [6]:
CHOD At least one track candidate
RICH Hit multiplicity: 5≤n≤32
MUV3 No hits (MUV3 is the most downstream muon veto)
LKr No more than one quadrant with energy deposit ELKr ≥5GeV
An optional additional contribution to the L0 trigger can be provided by
the LAV:
LAV No photons detected

3.3 The standard L0 trigger in NA62 45
Component Initial CHOD RICH MUV3 LKr L0 output
K+→π+π02140 1732 1179 1089 539 25.2 %
K+→µ+νµ6585 4204 3817 29 29 0.4 %
K+→π+π+π−579 458 225 180 171 29.5 %
K+→π+π0π0182 156 98 89 18 9.9 %
K+→π0e+νe525 403 253 248 84 16 %
K+→π0µ+νµ347 272 194 17 14 4.0 %
Total rate 7226 5765 1651 854 11.8 %
Table 3.2:
Rate of events inside NA62 acceptance after each step of L0 trigger. All rates
are expressed in
kHz
. Study performed with a set of
105
simulated events for each
K+
decay mode. The last line highlights the total event rate rescaled to the firing rate of the
CHOD detector, to which the beam upstream and downstream muon halos contribute as
well. Data from [6].
In the NA48 hodoscope, a primitive featuring at least one coincidence
between corresponding quadrants on the vertical and horizontal planes
defines a track candidate. Charged particles may start showers in the Liquid
Kripton Calorimeter: therefore, no multiple (spatially separated) energy de-
posit clusters are allowed on the LKr, since this would mean that more than
one pion have been detected, or protons or
e±
. This condition is intended
to set an upper limit to the number of hadrons detected in the same event.
However, the possibility of two showers clustering in the same sector of the
calorimeter, within its spatial resolution, limits the
2π
and
3π
rejection level
achievable in this way.
Table 3.2 reports the most recent simulation study of the rejection capa-
bility of each of the conditions listed above [6].
While the existence of a track detected by the CHOD sets the main
acceptance window, the condition on the multiplicity of hits on the RICH
detector effectively weakens the
3π
and beam halo components (the latter
is not shown in the table). Events featuring one or more
π0
are also partially
rejected in this way, due to frequent photon conversion. A slight increase of
π0
rejection would be enabled by the availability of LAV sub-detectors. The
condition on the LKr cluster multiplicity helps rejecting events with photons,
and the contribution of the most downstream muon veto sub-detector allows
for a muon suppression to the level of percent.

46 An online trigger using the RICH detector
3.4 Use of GPUs in triggers
Researchers from all over the world are beginning to develop GPU algo-
rithms for a variety of applications, including medicine, finance, chemistry,
experimental and theoretical physics, network science and many more. This
new branch of research is often referred to as
GPGPU
, i.e. General-Purpose
computing on Graphics Processing Units, a term coined in 2002 which refers
to an early trend of using GPUs for non-graphics applications [34].
High Energy Physics experiments rely on the acquisition and analysis of
large amounts of information. Modern particle detectors feature very fast
time responses, as required by the always increasing pace of accelerator
technology. Most detectors feature a binned bi- or tri-dimensional geometry,
providing accurate spatial information.
Such structured systems would natively benefit from parallel-oriented
analysis techniques. Moreover, particle physics computing is an intrinsically
parallel problem: experiments produce lots of of events, which are compu-
tationally local. Analysis is indeed carried out independently for each event
on different memory locations. Hence the use of multi-thread techniques is
expected to bring huge improvements in data processing.
Experiments such as ATLAS and ALICE at the LHC are starting to explore
the advantages of using GPU (Graphical Processing Unit) programming
in their High-Level Triggers (HLT), in order to perform faster analysis on
Terabytes of recorded data. In particular, a track selection algorithm was
developed for ALICE, that combines a fast Cellular Automaton
5
method
for pattern recognition and a Kalman Filter
6
for track fitting [30]. Kalman
Filters are also used in ATLAS to speed up the process of vertex finding.
ATLAS is also designing a parallelized version of a toolkit for Multi-Variate
Analysis of events [45,70].
The Bejing Spectrometer (BES-III) experiment at BEPC, designed to per-
form a thorough study of the spectra of light hadrons, is successfully using a
framework for partial wave analysis implemented on graphics processors
[15]. Other ion and nucleon spectroscopy facilities such as FAIR (Facility for
5
Cellular automata are discrete deterministic mathematical models for scientific compu-
tation. An automaton consists of a grid of cells whose evolution is a function of the current
state of the cell and its two immediate neighbors only.
6
A Kalman Filter is a statistical algorithm that produces an estimate of the system state
by evaluating several streams of “noisy” data.

3.5 The K+→π+π0background 47
Antiproton and Ion Research at the GSI in Darmstadt) already make use of
GPUs in their simulation and data analysis frameworks [52].
A project is being developed within the NA62 collaboration, which
aims to integrate GPUs into the lowest-level trigger for the first time in High
Energy Physics research. The use of GPUs in such a hard real-time system has
not been attempted so far, but it looks a realistic and challenging possibility.
The online use of GPUs would allow the computation of complex trigger
primitives while providing a highly scalable trigger architecture. Emergent
increased speed requirements would be handled just by adding more GPUs.
Cards with hundreds of parallel floating-point units are extremely powerful
hardware available at a relatively small cost, thanks to the continuous
development driven by the huge market of computer games and by the
broad excitement about GPGPU applications.
3.5 The K+→π+π0background
The aim of this work is to further reduce the rate of
K+→π+π0
events fed
to the L1 farm. This is the most prominent background after the standard
L0 trigger selection, as shown in Table 3.2.
Among the kinematically constrained backgrounds (see Chapter 1.4),
K+→π+π0
is the only process falling in the same missing mass region
as the signal. This
2−
body process features a closed kinematics and could
therefore be detected as a Dirac delta in the spectrum of the missing mass
in the decay of the beam kaon into
π+
(neglecting resolution effects). When
the distribution of experimental errors is convoluted with the expected
spectrum for this process, the squared missing mass
m2
miss
distributes as a
Gaussian around the squared mass of the neutral pion.
From an experimental point of view, the signature of the
K+→π+π0
process consists of one or more charged tracks detected (to account for the
charged pion and the eventual conversion of photons from π0decay).
This process may yield multiple ˇ
Cerenkov rings in case of:
•
inelastic scattering on the material of the beam pipe or of the upstream
detectors
•Dalitz decay of the neutral pion: π0→e+e−γ
•photon conversion γ→e+e−in a sufficiently upstream region.

48 An online trigger using the RICH detector
The identification of a ˇ
Cerenkov ring on the RICH detector provides
information on both the direction and the velocity of the particle that has
crossed the detector volume. In principle, the relationship between these
quantities can tell whether a detected pion comes from a 2-body decay or
not. Let us go through the kinematics involved in the K+→π+π0decay.
Let
PK
,
Pπ
and
P0
be the four-momenta of the kaon, of the charged
pion and of the neutral pion respectively. In the centre of mass frame, the
equality PK=Pπ+P0reads
mK=E∗
π+E∗
0
0 =
P∗
π+
P∗
0
(3.1)
where
E∗
π
and
E∗
0
are the centre of mass energies of the charged and neutral
pion respectively. The second relation can be written as
(E∗
π)2−m2
π= (E∗
0)2−m2
0(3.2)
and therefore, using the first of Eqns. 3.1, we find the centre of mass energy
of the π+, that is single-valued:
E∗
π=m2
K+m2
0−m2
π
2mK
(3.3)
Now consider the invariant product
Pµ
KPπµ
. In the rest frame of the
decaying kaon it reads
Pµ
KPπµ∗=mKE∗
π−
0·
P∗
π=mKE∗
π(3.4)
On the other hand, in the laboratory frame we have to consider the momenta
of both particles:
Pµ
KPπµ=EKEπ−
PK·
Pπ=EKEπ− |
PK||
Pπ|cos θKπ (3.5)
where θKπ is the angle comprised between the K+and the π+tracks.
The position of the ˇ
Cerenkov ring of the pion provides a measurement of
the direction of the pion, which can be related to
θKπ
by means of the simple
backwards propagation steps described in Chapter 4, and of the velocity
βπ
of the pion. Therefore, if we assume that the detected particle is really a
charged pion, we can compute its energy and momentum:
Eπ=γπmπ=mπ
1−β2
π
(3.6)
|
Pπ|=βπEπ=βπmπ
1−β2
π
(3.7)

3.6 Feasibility study 49
If we substitute Eqns. 3.6 and 3.7 in Eqn. 3.5, and match the two expres-
sions 3.4 and 3.5 for the
Pµ
KPπµ
invariant, we find that the velocity of the
pion is constrained by the laboratory-frame decay angle
θKπ
through the
relation
θKπ(βπ)K+→π+π0
= arccos 1
βπ|
PK|EK−mK
mπ
E∗
π1−β2
π(3.8)
that arises from the closed kinematics of 2-body decays.
In principle,
EK
and
|
PK|
are beam parameters that are known to a
precision of 1%; therefore, a RICH measurement alone would allow to check
if Eqn. 3.8 holds. In case of a positive result, a
K+→π+π0
event could be
identified and safely discarded.
3.6 Feasibility study
The GPU rejection algorithm for
K+→π+π0
events would add to the
hardware-implemented L0 trigger described in Section 3.3.
As a first step, I had to verify:
•
the resolution of the process of reconstructing the particle kinematic
variables by fitting a ˇ
Cerenkov ring to the hits on the photomultiplier
flanges;
•
the background rejection and signal acceptance: these quantities have
a strong dependence on the reconstruction resolution;
•
whether the data flow and algorithm execution chain speed can be
optimized in order to match the latency of the L0 trigger (1 ms).
Since positive results from such feasibility studies were a prerequisite
for the conception of the actual GPU algorithm, a thorough analysis was
performed by means of the NA62 software framework. The NA62 detector
is still being commissioned, therefore I have used Montecarlo simulations in
order to define the design of a RICH-based trigger. The results of this study
are reported in Chapter 5.
4
RICH reconstruction
Contents
4.1 Geometric corrections ................... 53
4.2 Track propagation: upstream magnets ......... 55
4.3 Reconstruction accuracy ................. 58
The project described in this thesis was partly carried out by means of
the NA62 software. “NA62FW”, i.e. the NA62 software suite, is still being
actively developed. It includes a Montecarlo event generator, featuring
Geant4
1
modelling and event reconstruction routines for most NA62 detec-
tors. This framework makes use of many Physics utility libraries: detector
geometry and particle propagation are implemented through Geant4 physics
lists, while some ROOT classes handle input/output and data processing,
and define hit and event structures. While this thesis was being developed,
hardly any Physics analysis algorithm was implemented in NA62FW. The au-
thor designed the reconstruction and track propagation methods described
in this Chapter.
In order to consider all the material in which particles could interact,
I simulated
K+→π+ν¯ν
and
K+→π+π0
decays enabling all the sub-
detectors upstream of the RICH, that was also included. I then used the
reconstruction routines supplied with the NA62 software to examine the
events detected by the RICH. Figure 4.1 shows a typical output of the RICH
reconstruction routine: a ˇ
Cerenkov cone emitted by a charged particle re-
sults in a ring of photomultipliers firing.
1
Geant4 is a toolkit to simulate the passage of particles through matter.
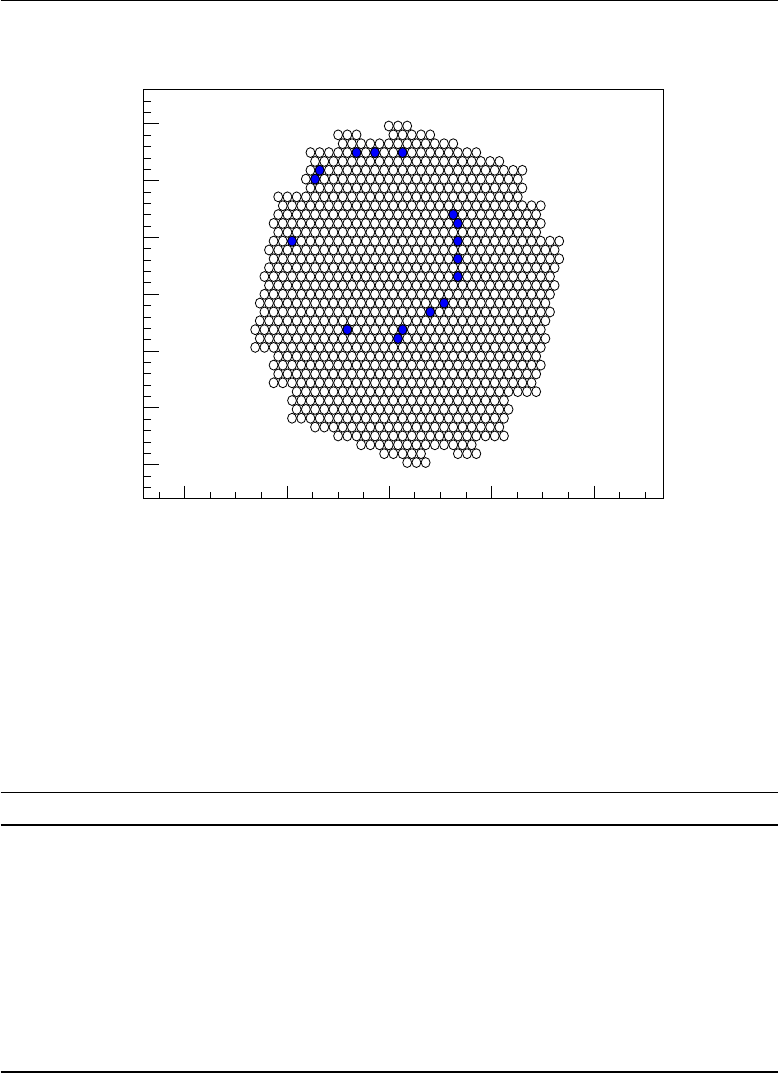
52 RICH reconstruction
x [mm]
1200 1400 1600 1800 2000
y [mm]
-300
-200
-100
0
100
200
300
Figure 4.1:
ˇ
Cerenkov ring produced by a simulated
π+
with momentum
15 ≤Pz≤35
GeV/con one of the two PM spots of the RICH. Each circle represents a photomultiplier.
The RICH reconstruction algorithm that was provided by the NA62 soft-
ware at the time of my work may be summarized as follows:
Algorithm 1: RICH event reconstruction
input : coordinates of a set of firing photomultipliers (RICH event)
output :ˇ
Cerenkov ring parameters (
C, R)and timestamp T
¯x,¯y←compute centre of gravity of the hits;
initial guess:
C←¯x,¯y
initial guess: R ←18.8 cm
fit circle(
C, R)to {hit}i=0...nγ
T←compute average time of the hits
Here,
¯x
and
¯y
are the coordinates of the centre of gravity of the hits,
C
is
the center of the fitted ring and
R
is its radius. This procedure shows some
clear limitations. In fact, it only tries to adapt a single ring to the whole set
of photon hits in input. RICH events often feature more than one charged

4.1 Geometric corrections 53
particle producing ˇ
Cerenkov rings. Moreover, the geometry of the detector
is not completely taken into account. Finally, the whole framework lacks
simulation and reconstruction of piled-up events.
Therefore, I modified the code provided, and took the geometry features
that were missing into consideration. I will briefly explain how I achieved
this in Section 4.1.
Events pile-up and the possibility of detecting more than one ring were
not included at this time. The strategy the experiment will adopt in order
to manage the time superposition of events is still evolving, and anyway it
does not represent a critical aspect of this project. Regarding the possible
multiplicity of ˇ
Cerenkov rings, a big effort has been put into the design of a
GPU-based ‘multiple rings’ fitting algorithm. However, during the previous
Montecarlo characterization step that allowed me to study the rejection
efficiency of such trigger algorithm, the presence of more than one ring was
represented simply as a high χ2in a single-ring fit.
My trigger algorithm requires some level of physics reconstruction on
top of the detection of a ˇ
Cerenkov ring. In fact, the kinematic quantities
involved in the decay process are modified by the MNP-33 magnet of the
STRAW spectrometer. In addition, the original direction of the decaying
kaon has to be taken into account when computing the laboratory-frame
decay angle
θKπ
. In Section 4.2 I will describe the procedure I used in
order to reconstruct physical information about the process responsible for
a detected RICH event.
4.1 Geometric corrections
The existing reconstruction algorithm included in the NA62 software did
not take into account that:
•
the vessel of the RICH detector is rotated with respect to the beam
line, in order to minimize the possibility that beam particles spill into
the detection volume (see Chapter 2.3.3). The rotation angle is tuned
on the magnetic kicks due to the GTK and STRAW dipoles.
•
the two mirrors reflecting photons onto the focal plane are tilted at
different angles relative to the vessel axis. This asymmetry is meant to
spread light onto the central regions of the photomultipliers flanges.
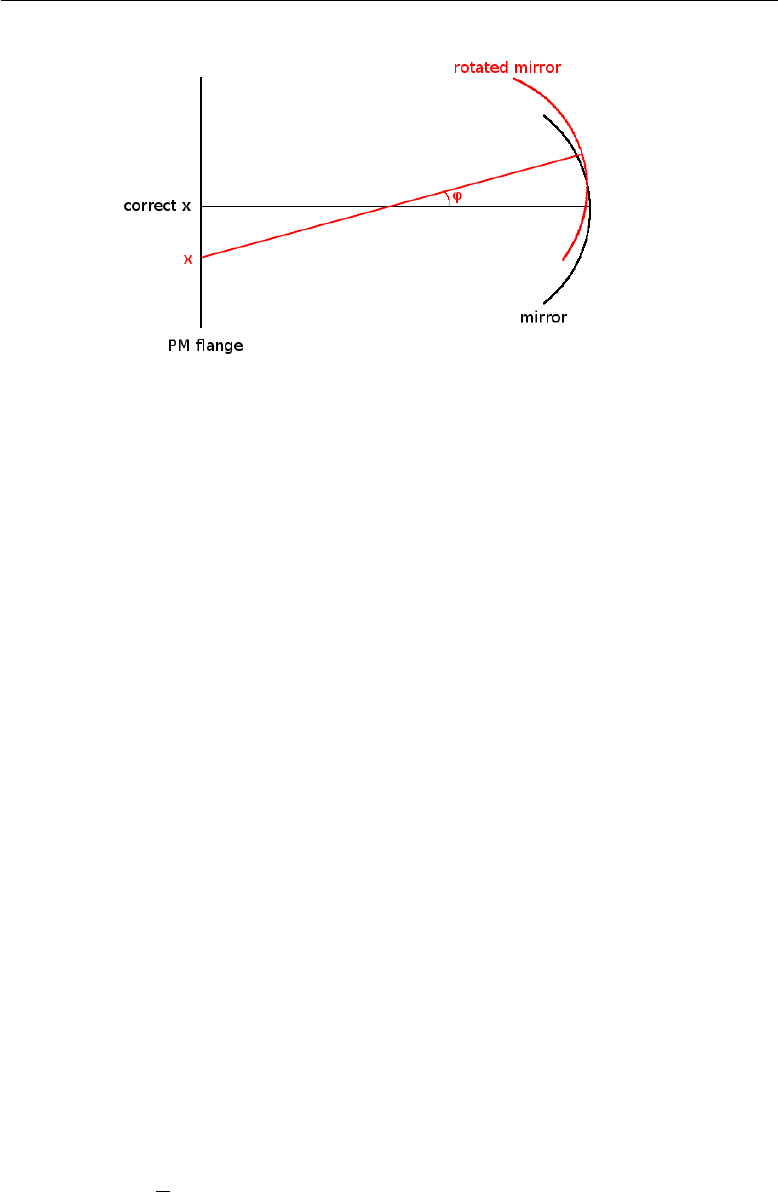
54 RICH reconstruction
Figure 4.2: Sketch representing the effects of the tilt of the RICH mirrors.
Figure 4.2 illustrates the rotation of the mirrors. The tilts applied to the
two mirrors are different, hence I corrected this effect on a hit-by-hit basis.
On the contrary, I fixed the global vessel rotation through a single operation
on the position of the centre of the ˇ
Cerenkov ring, that is the only parameter
affected.
The 1952 PMTs are placed on the RICH flanges so that the first 976 are
on the left-side frame, and the others on the right-side frame. Let
ϕ
and
ϕ
be the Salève and Jura mirrors angles to the vessel axis, respectively. Hit by
hit, I shift the
x
coordinate of the hit by a quantity
ϕR
or
ϕR
depending on
which spot is illuminated:
x≡x−2fϕ 0≤Channel ID <976
x−2fϕ976 ≤Channel ID <1052 (4.1)
where
f=R/2
is the focal lenght of the device, R being the curvature radius
of the mirrors.
Let us now see how to account for the global rotation of the vessel, repre-
sented in Figure 4.3. I treated this by shifting the centre of the reconstructed
ˇ
Cerenkov ring along the
x−
axis by an adequate quantity. Let
C= (x, y)
be
the centre
C
of the ring,
θx
be the direction of the particle projected onto
the
x−
axis of the laboratory frame, and
θ
x≡θx−θrich
the
x
component of
the direction of the particle in the RICH frame. The following relation holds:
tan θ
x=x
f(4.2)
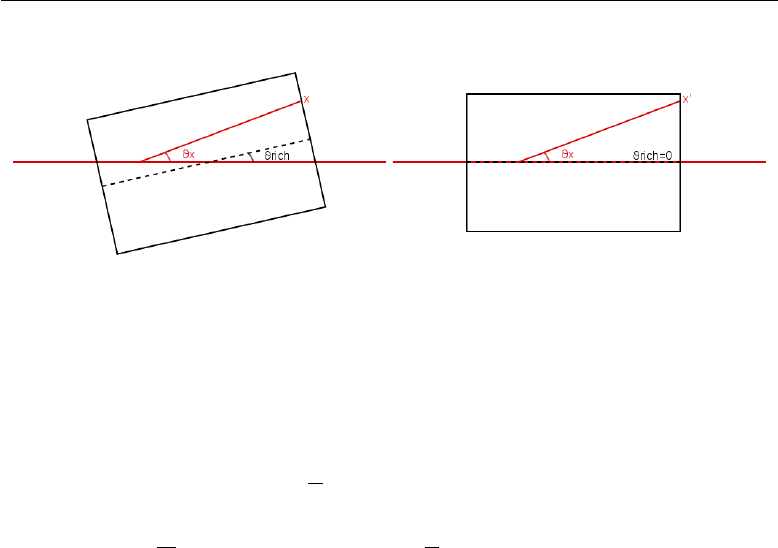
4.2 Track propagation: upstream magnets 55
(a) (b)
Figure 4.3: Sketch representing the effects of the rotation of the RICH vessel.
Therefore we can expand θxas:
θx=θ
x+θrich = arctan x
f+θrich (4.3)
tan θx≡x
f=⇒x=ftan arctan x
f+θrich(4.4)
The resulting
x
is the coordinate where the centre of the ring should
be moved to account for the vessel rotation. The
y
coordinate remains
unchanged.
These two simple geometrical corrections allow the achievement of an
angular resolution of the order of
σ(θx)≤450 µrad
. Figure 4.4 shows
the reconstruction accuracy achieved for simulated
K+→π+π0
events,
computed using 4 different subsets of data:
•events with hits on one spot only (Jura or Salève),
•events with rings spread across the two spots,
•the complete set of events.
4.2 Track propagation: upstream magnets
Through the assessment of the parameters of the ˇ
Cerenkov ring, we can now
compute the components of the direction of the particle crossing the RICH:
θx= arctan (x/f)(4.5)
θy= arctan (y/f )(4.6)
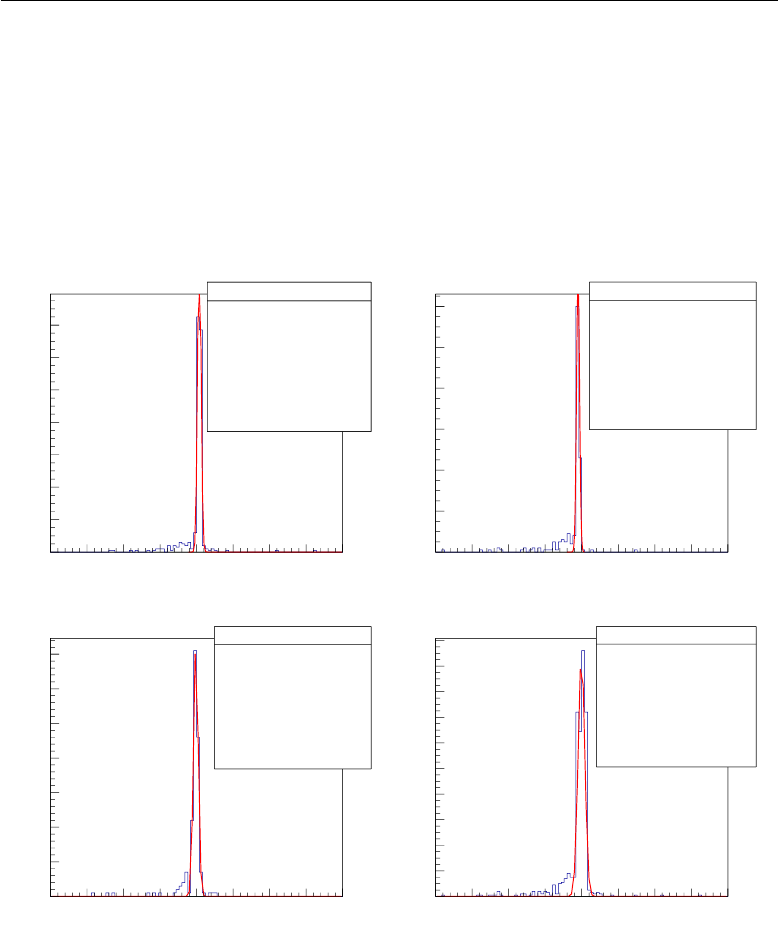
56 RICH reconstruction
xAngleRichResolutionSalev
Entries
354
Mean
-2.673e-06
RMS
0.001927
/ ndf
2
χ
19.03 / 10
Constant
15.4
±
204.2
Mean
0.000014
±
0.000379
Sigma
0.0000108
±
0.0002319
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
0
20
40
60
80
100
120
140
Entries
354
Mean
-2.673e-06
RMS
0.001927
/ ndf
2
χ
19.03 / 10
Constant
15.4
±
204.2
Mean
0.000014
±
0.000379
Sigma
0.0000108
±
0.0002319
RICH θx resolution
θx(MC) - θx(measured) [rad]
Salève side
xAngleRichResolutionJura
Entries
229
Mean
-0.001368
RMS
0.002519
/ ndf
2
χ
13.25 / 3
Constant
12.5
±
132.2
Mean
0.0000161
±
-0.0005039
Sigma
0.0000121
±
0.0002108
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
0
20
40
60
80
100
120
xAngleRichResolutionJura
Entries
229
Mean
-0.001368
RMS
0.002519
/ ndf
2
χ
13.25 / 3
Constant
12.5
±
132.2
Mean
0.0000161
±
-0.0005039
Sigma
0.0000121
±
0.0002108
RICH θx resolution
θx(MC) - θx(measured) [rad]
Jura side
xAngleRichResolutionBoth
Entries
174
Mean
-0.0005348
RMS
0.001895
/ ndf
2
χ
26.83 / 17
Constant
7.53
±
73.67
Mean
2.662e-05
±
-9.905e-05
Sigma
0.0000192
±
0.0003188
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
0
10
20
30
40
50
60
70
xAngleRichResolutionBoth
Entries
174
Mean
-0.0005348
RMS
0.001895
/ ndf
2
χ
26.83 / 17
Constant
7.53
±
73.67
Mean
2.662e-05
±
-9.905e-05
Sigma
0.0000192
±
0.0003188
RICH θx resolution
θx(MC) - θx(measured) [rad]
Rings spread
on both sides
xAngleRichResolutionAll
Entries
757
Mean
-0.0005379
RMS
0.002196
/ ndf
2
χ
220.6 / 36
Constant
9.7
±
189.8
Mean
2.182e-05
±
-3.653e-05
Sigma
0.0000125
±
0.0004511
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
0
20
40
60
80
100
120
140
160
180
200
xAngleRichResolutionAll
Entries
757
Mean
-0.0005379
RMS
0.002196
/ ndf
2
χ
220.6 / 36
Constant
9.7
±
189.8
Mean
2.182e-05
±
-3.653e-05
Sigma
0.0000125
±
0.0004511
RICH θx resolution
θx(MC) - θx(measured) [rad]
All data
Figure 4.4:
Resolution achieved on the
x
component of the direction of pions from
K+→π+π0crossing the RICH detector.

4.2 Track propagation: upstream magnets 57
where
x
and
y
are the coordinates of the ring centre, already corrected for
the RICH geometry as explained in Section 4.1.
In order to trace the decay angle
θKπ
back, we must propagate the
detected track backwards to the decay vertex. This implies reverting the
magnetic kick due to the dipole of the downstream spectrometer. If we
assume that the particle is a pion, we can compute the kick given to it
through the approximate formula
θkick =Pkick
Pπ(β)(4.7)
valid for small deflections (
|Pkick/Pπ| ≈ 10−2
in the fiducial momentum
region), where
Pπ(β) = βmπ/1−β2
. Notice that we are using the value
of
β
computed from the radius of the detected ˇ
Cerenkov ring (see Chap-
ter 2.3.3), introducing therefore an experimental uncertainty.
A sketch representing the original direction of the charged particle and
its direction after the spectrometer magnet is shown in Figure 4.5. Once
θkick
is computed, we may trace the original direction
θx,orig
back by subtracting
θkick from the direction θxat the RICH:
θx=θx,orig +θkick (4.8)
Like those described in the previous section, the corrections shown here
only modify the xcomponent of the direction of the particle.
Let us now assert the physical meaning of the angle we have just found.
Downstream of the Gigatracker, the beam spectrometer described in Chap-
ter 2, the emerging
K+
beam is bent at an angle
θK
on the
x
–
z
plane. The
angle
θx,orig
we have just computed does not represent the decay angle, i.e.
the angle between the decaying beam kaon and its charged daughter. All the
directions defined so far are relative to the
z−
axis of the laboratory frame,
that coincides with the direction of the beam upstream of the Gigatracker.
The relationship between the computed angle and the
x
component of the
true decay angle
θKπ
is shown in Figure 4.6, where I used the following
labels:
•θxπ
is the
x
component of the decay angle, i.e. of the angle measured
in the laboratory frame between the kaon and pion tracks;
•θx
is the angle measured between the direction of the detected particle
and the
z−
axis of the laboratory frame (
θx,orig
in the above formulas);
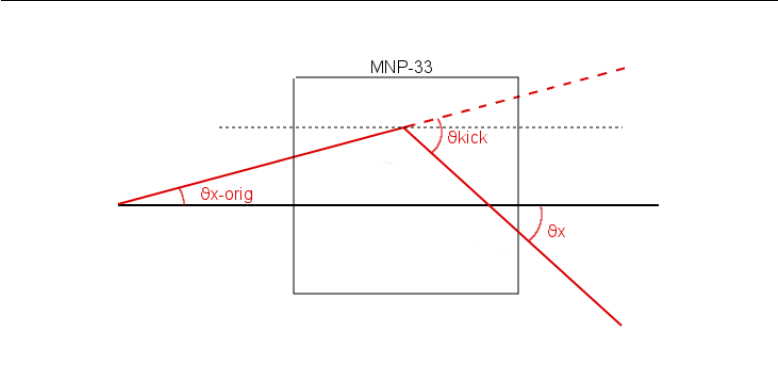
58 RICH reconstruction
Figure 4.5:
Sketch showing the effect of the spectrometer magnet on the direction of
charged particles.
•θK
is the direction of the beam, after being bent by the GTK magnet,
relative to the laboratory frame.
Reverting to the notation I have used so far, we observe that the original
decay angle θKπ can be obtained with the following formula:
θx(Kπ)=θx,orig −θkick −θK(4.9)
where
θx,orig
was defined in Eqn. 4.5,
θkick
is computed as in Eqn. 4.7, and
θKwas defined above.
4.3 Reconstruction accuracy
In the previous sections I examined the simple analysis chain I have used
in order to extract physics information from the RICH data. The relevant
parameters used are: [32]
•θrich = +0.00175571 rad
•Pkick =−270 MeV/c
•θK= +0.0012 rad
Let us summarize the outcome of the analysis.
•
The velocity of the particle is computed from the radius of the detected
ring as of Eqn. 2.14, and does not undergo any further modification.
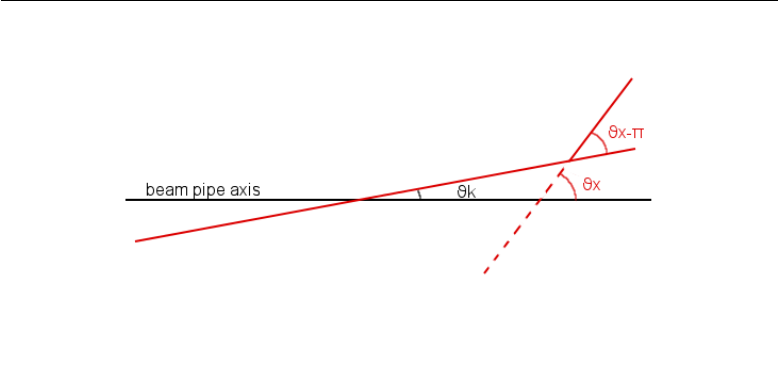
4.3 Reconstruction accuracy 59
Figure 4.6:
Sketch representing the decay angle
θKπ
in the laboratory frame and in the
rest frame of the decaying kaon.
•
The first adjustment performed consists in a hit-by-hit shift of the PMT
coordinates, needed in order to take the mirrors tilt into account.
•
Once the hits are repositioned, we can fit a ring to the data. We then
change the
x
coordinate of the found ring centre according to Eqn. 4.4.
•
We now use the
x
and
y
coordinates to compute the
θx, θy
components
of the particle direction (Eqns. 4.5,4.6). Of these,
θx
is propagated
back according to Eqn. 4.9.
We finally obtain the decay angle:
θ2
Kπ =θx2
(Kπ)+θ2
y(4.10)
Figure 4.7 shows the accuracy achieved in the reconstruction of
βπ
and
θKπ
. The decay angle is reconstructed with a resolution
σ(θKπ)≈650 µrad
(Figure 4.7(a)). On the other hand, the distribution of
β
(Figure 4.7(b))
shows a slight asymmetry towards values higher than the true speed of
the particle. This is probably due to an uneliminable effect of the discrete
binning of photomultipliers. The asymmetry arises as the ˇ
Cerenkov light
emission angle is generally overestimated, as it can be inferred from Fig-
ure 4.8. In fact, the distributions shown here were obtained by use of the
Taubin algorithm for circle fitting, described in Appendix A.3.1, which is one
of the most robust single-ring fit procedures available with respect to the
radius of the circle. Quoting the RMS of the distribution as a measurement
of the reconstruction accuracy, we may state that the resolution in
β
is
approximately σ(β)≈5×10−6.

60 RICH reconstruction
theta_m_err
Entries 6832
Mean -0.0001908
RMS 0.002397
/ ndf
2
χ 893.5 / 74
Constant 23.2± 1018
Mean 0.0000103± -0.0001891
Sigma 0.0000107± 0.0006445
(measured) [rad]
πK
θ(MC truth) -
πK
θ
-0.02 -0.015 -0.01 -0.005 0 0.005 0.01 0.015 0.02
A. u.
0
200
400
600
800
1000
theta_m_err
Entries 6832
Mean -0.0001908
RMS 0.002397
/ ndf
2
χ 893.5 / 74
Constant 23.2± 1018
Mean 0.0000103± -0.0001891
Sigma 0.0000107± 0.0006445
Decay angle resolution
(a) Decay angle resolution
beta_m_err
Entries 6832
Mean -2.074e-06
RMS 4.93e-06
(measured)
π
β(MC truth) -
π
β
-20 -15 -10 -5 0 5 10 15 20
-6
10×
A. u.
0
100
200
300
400
500
600
700
beta_m_err
Entries 6832
Mean -2.074e-06
RMS 4.93e-06
Pion velocity resolution
(b) Particle speed resolution
Figure 4.7: RICH reconstruction resolution.
Let us finally discuss a few critical aspects concerning this analysis. At
the beginning of this section, the magnetic kick due to the spectrometer
dipole was computed assuming the detected particle is a
π+
, therefore
using its mass in Eqn. 4.7. In fact, most events without pions will be
rejected by the hardware L0 trigger. However, on some occasions we might
still wrongly assume a particle is a pion and propagate it with a wrong
formula. This would not in any way affect the efficiency for the signal of the
trigger presented in this thesis, since events without charged pions would
be discarded during the stage of offline analysis. Besides, the Montecarlo
study reported in this work does not examine background channels different
from
K+→π+π0
, as the analysis process involved would be substantially
different.
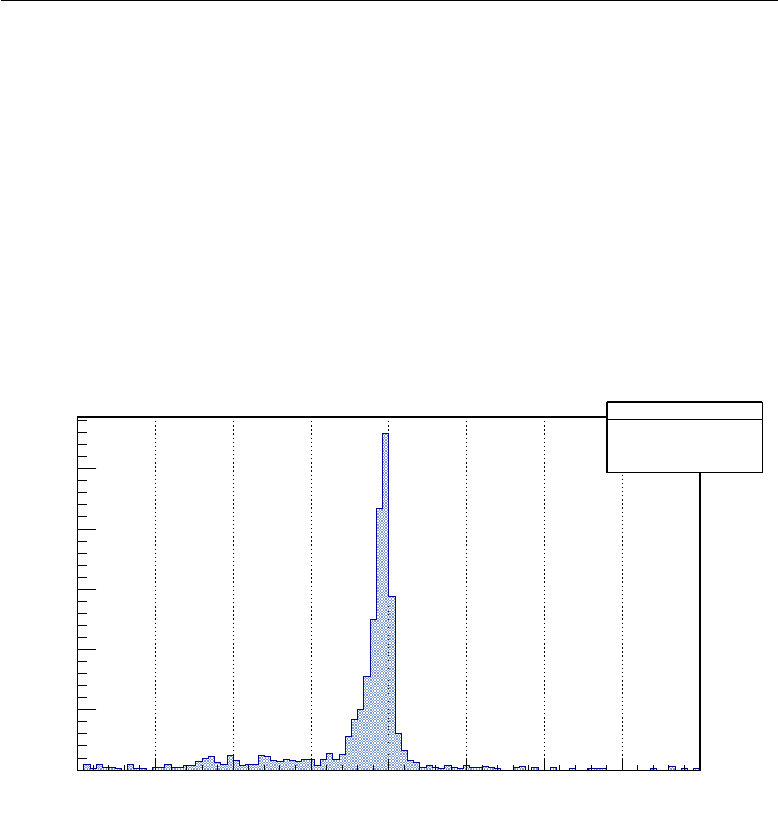
4.3 Reconstruction accuracy 61
cherenkov_angle
Entries 1368
Mean -0.0003644
RMS 0.0008673
(RICH) [rad]
C
θ(MC truth) -
C
θ
-0.004 -0.003 -0.002 -0.001 0 0.001 0.002 0.003 0.004
A. u.
0
50
100
150
200
250
cherenkov_angle
Entries 1368
Mean -0.0003644
RMS 0.0008673 events
0
π
+
π2k
Cherenkov angle resolution
events
0
π
+
π2k
Figure 4.8:
Reconstruction resolution on the ˇ
Cerenkov light emission angle. An asymmetry
is clearly visible between RICH reconstructed data and the “Montecarlo truth”.

5
Trigger characterization
Contents
5.1 βπ−θKπ correlation ................... 63
5.2 Missing mass ........................ 65
5.3 ˇ
Cerenkov ring radius ................... 68
5.4 Other possible optimizations ............... 69
5.5 Performance together with the standard L0 trigger . . 72
In order to achieve background rejection while preserving as much signal
as possible, we must look for a set of variables whose distribution allows to
separate
K+→π+ν¯ν
events from the target background
K+→π+π0
. We
may then set appropriate cuts on these distributions, and transmit to higher
trigger levels only the portion of data fulfilling these requirements.
5.1 βπ−θKπ correlation
In Chapter 3.5 I outlined the kinematics of the
K+→π+π0
decay and
introduced Eqn. 3.8, that could be used to identify this background. The
K+→π+ν¯ν
decay is a 3-body process, and therefore its kinematics is
not constrained. Background rejection could be obtained by determining
(θKπ)2−body
as a function of the RICH-measured
βπ
for each event, and dis-
carding those events whose reconstructed
θKπ
, computed from the direction
θπdetected at the RICH, is close to (θK π )2−body.
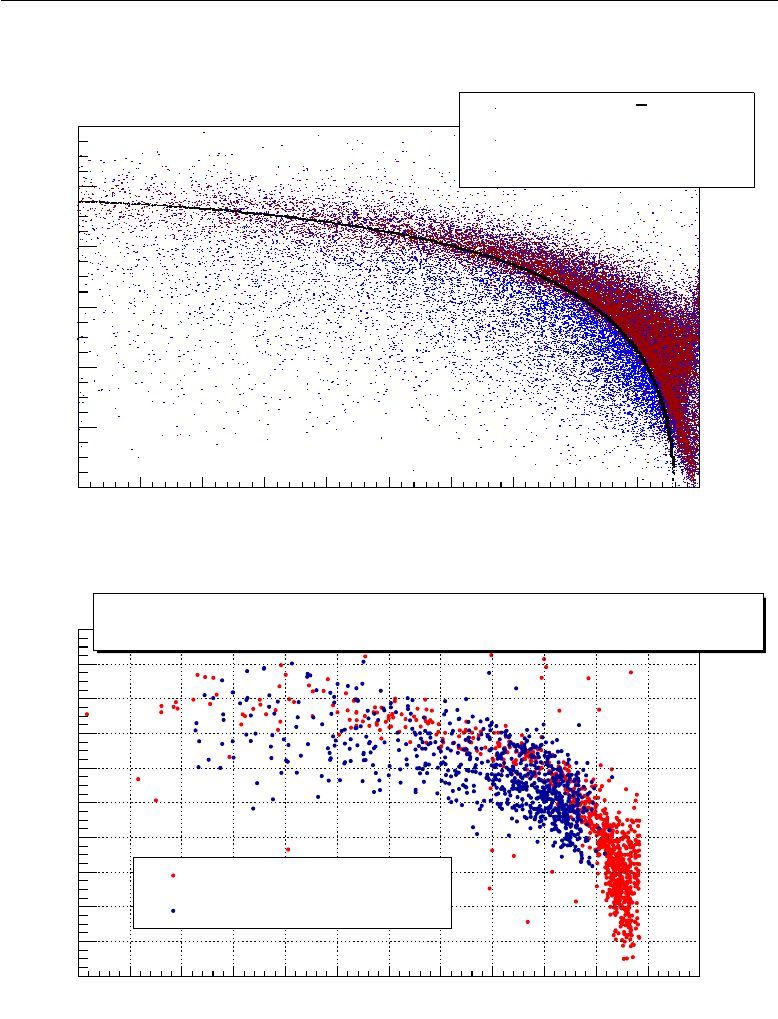
64 Trigger characterization
π
β
0.99995 0.999955 0.99996 0.999965 0.99997 0.999975 0.99998 0.999985 0.99999 0.999995 1
(rad)
πK
θ
0
0.002
0.004
0.006
0.008
0.01
0.012 ν ν
+
π →
+
K
0
π
+
π →
+
K
(expected)
0
π
+
π →
+
K
No signal cuts
(a)
RICH ring radius [cm]
80 90 100 110 120 130 140 150 160 170 180 190 200
RICH ring distance from beam axis [cm]
0
20
40
60
80
100
120
140
160
180
200
after L0 cut
0
π
+
π →
+
K
Signal after L0 cut
track propagation
+
πDistance from beam axis recomputed after
track propagation in GTK
+
in MNP-33 and K
(b)
Figure 5.1:
Top plot
(a)
: the distributions of the signal and of the
π+π0
background in the
(θKπ )2−body −βπ
plane. Bottom plot
(b)
: the same plane is remapped to the raw ˇ
Cerenkov
ring observables, and L0 trigger and standard signal cuts (see Table 5.1) are applied to the
data sets.

5.2 Missing mass 65
Unfortunately, the Montecarlo simulations I will report in this chapter
have revealed that the resolution of the RICH is not sufficient to successfully
exploit this approach. In Figure 5.1(a), the black dots corresponds to the
exact mathematical relation between the decay angle and the velocity of
the pion for the
K+→π+π0
decay, described in Eqn. 3.8. The red dots
correspond to RICH-reconstructed
(βπ, θKπ)
pairs, computed as described in
Chapter 4, for simulated
π+π0
events, while blue dots represent simulated
π+ν¯νevents.
It can be inferred from Figure 5.1(a) that:
•π+π0
events (red dots) cover a wide area of the
(θKπ)2−body −βπ
plane,
and there is a slight asymmetry compared to the expected occupancy
(black dots); this means that the resolution of a single detector might
not be sufficient to perform such bi-dimensional selection.
•
The regions occupied by the two data sets – signal (blue) and
π+π0
background (red) – completely overlap.
It follows that a significant bi-dimensional cut set up on relation 3.8 would
reject a large amount of signal events, and therefore it is not feasible.
Figure 5.1(b) is a re-parametrisation of the plot shown in 5.1(a). Here,
the radius and position of the ˇ
Cerenkov ring are put in the relation emerging
from Eqn. 3.8:
d(rc) = d(θ(β(rc))) (5.1)
where
d(θ)
is the ring centre distance to the focus, defined in Eqn. 2.12,
θ(β)
was defined in Eqn. 3.8,
β(rc)
in Eqns. 2.11 and 2.7 and
rc
is the ˇ
Cerenkov
ring radius. The aim of this test was to understand if the spread of the
distributions of Figure 5.1(a) was due to the intrinsic resolution of the RICH
detector or if it was a consequence of computational issues arising during
the evaluation of
βπ
and
θKπ
. From Figure 5.1(b) we see that such spread is
due to the finite resolution of the RICH, and unfortunately this issue cannot
be overcome in the contest of a real-time trigger. Moreover, the signal
selection and standard L0 trigger cuts applied in this plot have the effect
of thinning the area covered by
πν¯ν
data, thus making a bi-dimensional
selection of π+π0unattainable.
5.2 Missing mass
In principle, what best distinguishes a 3-body from a 2-body decay is the
energy spectrum of the decay products. In a 2-body decay, the energy spec-

66 Trigger characterization
trum of the
π+
in the rest frame of the decaying kaon is single-valued (see
Chapter 3.5).
Instead, for a 3-body decay (such as the signal) the rest frame energy
of the
π+
belongs to a continuum that spreads roughly from
mK−mπ
to
as near to zero as our detectors can measure (the mass of the neutrinos is
negligible with respect to the precision of these instruments). Figure 1.5
shows the shapes of the squared missing mass to the detected pair
(K+, π+)
for the target process and the most important K+decay modes.
For the two-body decay this quantity is theoretically expected to dis-
tribute as a Dirac delta centred in
m2
π00.0182 GeV2/c4
. Taking the finite
resolution of our detectors into account, we expect a Gaussian distribution
around this value.
I explored the possibility of using the missing mass, computed using
exclusively the information originating from the RICH detector, as a cut
variable. However, as shown in Figure 5.2, due to the limited momentum
resolution of the RICH it is not possible to separate the two processes this
way either. In fact, the two sets of simulated events (respectively signal and
π+π0background) end up in wide superposition on this variable.
At the final level of data analysis, NA62 expects to put strong contraints
on the events to be tagged as signal. These should be set as follows:
•15 ≤Pπ≤35 GeV/c
, i.e. the range of momenta for which the
µ
–
π
separation achieved is maximum (
Pπ≥15 GeV/c
), with an upper
limit that ensures that the other particles from
K+
decay carry a
momentum of at least 40
GeV/c
and are therefore detectable. This
way, for example, at least one photon from
π0→γγ
decay is bound to
fall in the acceptance of the NA62 detector.
•105 ≤zvtx ≤165 m
, where
zvtx
is the
z
coordinate of the decay vertex,
i.e. the K+decay happened in the fiducial region.
•m2
miss ∈R1= (0,0.01)
or
∈R2= (0.026,0.068) GeV2/c4
, in order to
explore only “background-free” regions (see Figure 1.5).
Events not fulfilling these requirements will be left out of the fiducial
sample for data analysis. Such events would be discarded in any case at a
later stage, but we may exploit the signal selection to reject them already at
the online L0 stage. This will obviously reduce the amount of data fed to
higher level triggers, thus allowing more efficient evaluations at those stages.
5.2 Missing mass 67
]
2
[GeV
+
π and
+
to the K
miss
2
M
-0.14 -0.12 -0.1 -0.08 -0.06 -0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14
A. u.
0
10
20
30
40
50
after L0 cut
0
π
+
π →
+
K
Signal after L0 cut
Signal definition:
eventsν ν
+
π →
+
K
35 GeV≤
z
P≤15
165 m≤
vtx
z≤105
2
R∈ or
1
R∈
miss
2
M
2
= (0.00, 0.01) GeV
1
R
2
= (0.026, 0.068) GeV
2
R
Figure 5.2:
Spectrum of the missing mass to the
K+
and
π+
for the signal and the
K+→π+π0
background. The missing mass was computed using the information from
the rings detected on the RICH, assuming that the particle crossing the detector was a
π+
.
These spectra were obtained from the superposition of two sets of simulated events, one
containing only K+→π+ν¯νand one only K+→π+π0decays.
68 Trigger characterization
RICH ring radius [mm]
0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300
A. u.
0
50
100
150
200
250 after L0 cut
0
π
+
π →
+
K
Signal after L0 cut
Signal definition:
eventsν ν
+
π →
+
K
35 GeV≤
z
P≤15
165 m≤
vtx
z≤105
2
R∈ or
1
R∈
miss
2
M
2
= (0.00, 0.01) GeV
1
R
2
= (0.026, 0.068) GeV
2
R
Figure 5.3:
Reconstructed ˇ
Cerenkov ring radius for the signal and the
K+→π+π0
background after L0 cuts have been applied (Montecarlo-simulated data).
5.3 ˇ
Cerenkov ring radius
First of all, we notice that the signal is distributed along a limited range of
momenta, 15 to 35
GeV/c
. This means that the velocity of a charged particle
should be in a range defined by its mass, in order for the particle not to be
discarded. In the RICH detector, this results in limits to the radius of the
ˇ
Cerenkov rings. A Montecarlo simulation performed with the NA62 software
allowed me to find the distributions of the radius of the ˇ
Cerenkov rings for
signal and background events. The results are shown in Figure 5.3, where
we can see that this quantity provides a good option for events separation.
In particular, we can see that the peak value of the ˇ
Cerenkov radius is on
average larger for π+π0events than it is for K+→π+ν¯νevents.
If the signal had not been momentum-selected, we would have expected
the peak of
π+π0
events to be lower than that of the signal, due to the differ-
ent kinematics of the two processes. In the two-body decay, the charged and
neutral pion masses are similar, and therefore they carry similar fractions of
the kaon energy, about 50% each in the rest frame of the kaon. On the other
hand, the sought 3-body decay with two neutrinos contains only one pion,
and it is the only particle with a mass of the same order of magnitude as that

5.4 Other possible optimizations 69
β
0.99994 0.99995 0.99996 0.99997 0.99998 0.99999 1.00000
[cm]
c
R
0
2
4
6
8
10
12
14
16
18
βn
1
-1
cos = f tan
c
θ = f tan
c
R
Figure 5.4:
Expected radius of the ˇ
Cerenkov ring for a range of velocities from
β= 1/n
to
β= 1
. In this study I used
f= 17 m
and
n= 1.0000613422636
, the design values of the
RICH detector for NA62.
of the kaon. In this case, the larger fraction of the kaon energy is statistically
carried by the pion, and smaller fractions contribute energy to the neutrinos.
As a consequence, in the
K+→π+ν¯ν
decay the
π+
is on average faster than
when originating from
K+→π+π0
events. A higher velocity
β
produces
larger circles on the focal plane of the RICH detector, as shown in Figure 5.4.
However, the fiducial momentum region defined for the signal allows us
to discard a priori those events where the detected pion has a momentum
greater than 35
GeV/c
. This way, as Figure 5.3 suggests, we can suppress a
major component of the π+π0background.
5.4 Other possible optimizations
As discussed in Section 2.3.3, the RICH detector not only allows to perform
particle identification by distinguishing between muons and pions: it also
provides information about the flight direction of the charged particle cross-
ing its volume. Figure 5.2 shows that it is inefficient to use the missing mass
as a discriminating variable, with the resolution available online. However,
there may be some other variables which could exploit the whole informa-
tion we get from both the detection and our understanding of the decay

70 Trigger characterization
process responsible for
π+π0
events. Herein I will show how to look for such
variables and to exploit them. The results achieved so far have only provided
marginal improvements to the background rejection level already obtained.
This approach necessarily involves mathematical difficulties; nevertheless,
even a numerical approximation, if found, could provide interesting results
in the future.
In the two-body decay scenario, the correlation between the ring radius
and the position of its centre, that reflects the one existing between the
momentum and angle of the
π+
(see Chapter 3.5), would be a valuable
way to separate signal from background. However, it also causes difficult
computational issues. In fact, the variance is greater for a function of two
correlated variables than it is for a function of uncorrelated variables. Such
variance can be computed according to the general error propagation for-
mula.
Given a set
x
of
n
random variables with expectation values
µ
, and a
function f(x), assuming we can perform a Taylor expansion around µ:
f(x) = f(µ) +
n
i=1
(xi−µi)∂f
∂xix=µ
+. . . (5.2)
Truncating at first order:
E(f) =f(µ) + . . . (5.3)
Var(f) =E (f−E(f))2(5.4)
=E (f(x)−f(µ))2(5.5)
n
i=1
n
j=1 ∂f
∂xi
∂f
∂xjx=µVarij (x)(5.6)
For a function fof two variables xand y:
Var(f) = σ2
x∂f
∂xx=µ2
+σ2
y∂f
∂y x=µ2
+ 2 Cov(x, y)∂f
∂x
∂f
∂y x=µ
(5.7)
In the case of the missing mass, the small RMSs in the reconstructed
kinematic variables
βπ
and
θKπ
add up in a nonlinear way, thus making it
an unconvenient statistical variable from a computational point of view.

5.4 Other possible optimizations 71
The RICH reconstruction algorithm as it is now implemented exhibits
a slight asymmetry in the reconstruction of the particle velocity
β
, which
is usually overestimated (as shown in Figure 4.7 in Chapter 4.3). This
results in an inaccurate estimate of the particle flight direction, through the
assessment of its momentum
P(β, mπ)
and the backwards propagation of
the track across the two upstream magnets (see Chapter 4). In particular,
the magnitude of the magnetic deflection due to the spectrometer magnet
is inversely proportional to the momentum of the particle. The correlated
deviations of the reconstructed position and radius of the ˇ
Cerenkov rings
therefore add up when used to compute functions
f(βπ, θKπ)
of both vari-
ables, e.g. the function evaluating the missing mass m2
miss(K+, π+).
The problem of finding the function
g(βπ, θKπ )
that makes use of as much
information as possible while keeping its variance low is very interesting
from a mathematical point of view. Minimizing a functional (
Var(f)
in this
case) is a variational problem without a general solution. Unfortunately,
our knowledge is limited to the covariance matrix of the two variables, and
this does not allow for an algebraic solution to this problem. Moreover,
in the 2-body decay
βπ
and
θKπ
are not only strongly correlated, but also
functionally dependent. Therefore, the only reasonable solution would be a
variable obtained with as few computation steps as possible, but containing
full information about the physical process: for example
δ≡θKπ −θKπ(βπ)(5.8)
would exploit the functional relation between
θKπ
and
βπ
in the
K+→π+π0
decay, while preventing further computational steps that might increase the
variance of the test variable.
It is expected that the distribution of
δ
for
π+π0
events is peaked at 0.
On the other hand, nothing can be said a priori about the distribution of
δ
for events
π+ν¯ν
, which do not feature such functional dependence. The
width of the distribution for background events might be small enough to
allow a cut in a short range around 0.
Unfortunately, this is not a completely acceptable solution either, as
shown by the simulation results reported in Figure 5.5. The distribution
in
δ
for the signal events, in fact, is very narrow and centred so close to
0 that it almost completely overlaps the peak arising from
π+π0
events.
Furthermore, the signal lies in the momentum range for which the RICH
provides maximum accuracy in the reconstruction of
β
; since this is not true

72 Trigger characterization
) [rad]
meas
π
β(
πK
θ -
meas
πK
θ
-0.02 -0.015 -0.01 -0.005 0 0.005 0.01 0.015 0.02
A. u.
0
20
40
60
80
100
120
events after L0 cut
0
π
+
π →
+
K
Signal after L0 cut
Signal definition:
eventsν ν
+
π →
+
K
35 GeV≤
z
P≤15
165 m≤
vtx
z≤105
R2∈ R1 or ∈
miss
2
M
2
R1 = (0.00, 0.01) GeV
2
R2 = (0.026, 0.068) GeV
Figure 5.5: Distribution of δdefined in Eqn. 5.8 for signal and background events sets.
for the background, an asymmetry arises in the reconstruction of
β
, that
spreads the corresponding distribution towards the positive side.
However, we may once more exploit the fact that the background is
not filtered according to the pion momentum, and remove those events for
which the reconstruction asymmetry exceeds a given threshold from the
data pool, for example by requiring δ≤0.002 at trigger level.
5.5 Performance together with the standard L0
trigger
According to the distributions presented in the previous sections, the rejec-
tion power of the RICH-based trigger algorithm I developed for the NA62
experiment mostly emerges from a selection of the radius of the ˇ
Cerenkov
rings. Therefore, I performed a study on the rejection achievable with the
cut
Rc≤Rth (5.9)
Table 5.2 shows both the signal acceptance and the background rejection
for various threshold values. The first column lists the threshold values
Rth

5.5 Performance together with the standard L0 trigger 73
Signal definition:
Event type K+→π+ν¯ν
π+momentum along z15 to 35 GeV/c
Decay vertex zposition 105 to 165 m
Square missing mass to the K+and π+0 to 0.01 GeV2/c4
0.026 to 0.068 GeV2/c4
Table 5.1:
Offline analisys requirements for the selection of
K+→π+ν¯ν
events in the
NA62 experiment.
used. The second column shows the percentage of signal events that pass
the selection, computed as
npass/ntot
. The signal is selected according to the
requirements listed on Table 5.1. The third column shows the
π+π0
rejection
capability of the RICH-based L0 algorithm alone, which in this study consists
in the Rc≤Rth cut only. The rejection power is computed as 1−npass/ntot.
The “RICH
|
L0” column is the most significant one. It highlights the rejec-
tion power of my algorithm rescaled to the background events that have
passed the selection performed by the standard hardware L0 trigger. Finally,
the last column shows the combined rejection level achieved by the two
trigger algorithms – RICH-based and standard L0 – running in parallel. The
last row shows the
π+π0
background rejection achieved by the standard
hardware L0 trigger described in Chapter 3.3.
The selection performed by the
Rc≤Rth
requirement makes use of
different observables than the existing hardware-based L0 trigger, and it
makes it possible to cut the data rate fed to the following trigger stage by
an additional 60% to 70%. Such reduction may in turn allow the L1 stage
to perform deeper analisys, without stretching its latency or increasing the
amount of resources required.
The boldface row in Table 5.2 is an attempt to select a starting work-
ing point for further studies, as a reasonable compromise between signal
efficiency and backround rejection. The efficiency for the signal for the
quoted
Rth = 17.9cm
is (98.6
±
0.4)%, which means that the signal will
remain essentially unchanged. The background rejection achieved over the
L0 trigger is (64.8
±
1.2)% and the overall
π+π0
rejection adds up to (91.8
±0.2)%.

74 Trigger characterization
Rth (cm) Signal efficiency RICH rejection RICH |L0 L0+RICH
17.60 92.6 ±0.8 63.4 ±0.5 70 ±1 93.0 ±0.2
17.70 96.0 ±0.6 61.3 ±0.5 68 ±1 92.6 ±0.2
17.75 97.1 ±0.6 59.8 ±0.6 68 ±1 92.5 ±0.2
17.80 97.6 ±0.5 58.5 ±0.6 67 ±1 92.3 ±0.2
17.85 98.3 ±0.4 56.8 ±0.7 66 ±1 92.1 ±0.2
17.90 98.6 ±0.4 55.2 ±0.8 65 ±1 91.8 ±0.2
17.95 99.0 ±0.4 53.3 ±0.8 64 ±1 91.5 ±0.2
18.00 99.5 ±0.3 51.3 ±0.8 62 ±1 91.2 ±0.2
18.10 99.6 ±0.3 47.0 ±1.0 59 ±1 90.4 ±0.3
Standard L0 rejection 76.7 ±0.04
Table 5.2:
Rejection power and signal acceptance achievable with a cut on the radius of
ˇ
Cerenkov rings. All values are expressed as percentages, and the errors shown are pure
statistical uncertainties due to the size of the data samples. The last row shows the
π+π0
background rejection achieved by the standard hardware L0 trigger. For this study I used
two separate data sets consisting of 10000
K+
decays each. One data set contained only
π+ν¯νevents, while the other one consisted of K+→π+π0decays.
In a subsequent study I tried to estimate the effect of a cut on the
δ
variable introduced in Section 5.4. This selection does not add much to
that on the ˇ
Cerenkov radius, as it operates on correlated variables: the
faster a pion crosses the RICH detector, the worse its characteristics can be
measured. However, I found out that a cut
Rc≤17.9cm (5.10)
δ≤0.0025 (5.11)
yields a maximum
π+π0
rejection of (71.5
±
0.9)% on particles that passed
the standard L0 selection, while a cut
Rc≤17.9cm (5.12)
δ≤0.002 (5.13)
yields a slightly higher rejection of (72
±
1)%, maintaining a signal accep-
tance of (98.0 ±0.4)%.
Finally, I introduced a “ring fit quality” selection. A greater background
rejection can be expected if there is a possibility of detecting the presence of
more than one ˇ
Cerenkov ring, for the reasons explained in Chapter 3.5.

5.5 Performance together with the standard L0 trigger 75
The simplest way to check if the hits detected belong to one or more
rings is to perform a cut on a
χ2
variable computed on the result of the
ring fit. Montecarlo simulations show that a threshold
χ2
th = 1
allows to
discriminate between clean 1-ring events and multi-ring or noisy events.
Higher values of
χ2
th
did not sensibly change the result. The following cuts:
Rc≤17.9cm (5.14)
δ≤0.002 (5.15)
χ2
ring ≤1(5.16)
therefore allow to attain (77
±
1)% additional
π+π0
rejection after the
standard L0 cuts, with (96.2 ±0.7)% signal acceptance.
These numbers should be interpreted as the best achievable with a RICH-
based online trigger, since both the characteristics of the target processes
and the acceptance and resolution of this detector are taken into account.
Part III
Algorithm development and test

6
“Ptolemy”, a two-step algorithm
Contents
6.1 The necessity for a multi-ring algorithm ........ 79
6.2 Ptolemy’s theorem ..................... 82
6.3 Reparametrization of the photomultipliers lattice . . . 83
6.4 Pattern recognition .................... 86
6.5 Single-ring fit ........................ 89
6.1 The necessity for a multi-ring algorithm
In order to be used as lowest-level trigger, a ring-fitting algorithm needs to
be:
•seedless
: it will be fed with raw RICH data, with no previous infor-
mation on the ring position from other detectors;
•fast
: it will run concurrently with the hardware L0 trigger, with a
maximum latency (decision making time) of 1
ms
and an event rate of
about 10 MHz;
•accurate
: while the aim of this project is to reduce the background
events rate to as low as possible, we still need to maintain the signal
acceptance close to 100%. Our constraints therefore will be defined
by the finite combined resolution of the RICH detector and of the ring
finding algorithm;

80 “Ptolemy”, a two-step algorithm
•“multi-ring friendly”
, to account for inelastic hadron scattering and
π0
Dalitz decays, for the
π+π−π+
background, and to allow positive
identification of rare di-lepton decay modes.
When I started working on this thesis, there were no multi-ring parallel
fitting algorithms in literature ready to be adapted to RICH applications. For
this reason, I tried to figure out how to discard events with more than one
ring, i.e. with more than one charged track, that would be rejected during
the final K+→π+ν¯νanalysis.
If there are only single-ring algorithms available, the easiest way to check
whether the data points really belong to a single circle is to compute a
χ2
variable on the ring candidate. Except in the rare case when two rings are
concentric and similar in radius, a least squares analysis will return a higher
χ2when the points do not belong to the same ring.
However, as reported in Chapter 5, a background rejection algorithm is
more effective if it is designed to provide at least basic kinematical informa-
tion. The background process
K+→π+π0
analysed in this work may create
multiple rings in the cases reported in Chapter 3.5. The presence of more
rings (or parts of rings), and possibly of noise hits on the photomultipliers,
would make it difficult to evaluate the radius and position of a “real”
π+
ˇ
Cerenkov ring.
In addition, NA62 is a promising experiment for the study of other
K
decay channels, besides
π+ν¯ν
: the large statistics it will collect will make
it possible to probe other ultra-rare or forbidden decay channels with un-
precedented precision. Most current BSM theories predict some degree
of Lepton Flavour Violation (LFV). A non-exhaustive list of such theories
includes Supersymmetry (SUSY), Technicolor, Little Higgs models, extra
dimensions and even the introduction of heavy neutrinos.
SM-forbidden decays such as
K+→π+µ±e∓
and
K+→π−++
(with
, =µ, e
) would feature a very clean experimental signature. The high
statistics of NA62 – of the order of
1013
kaon decays – would allow the
current limits to be improved by a factor of about 10: the existing limits for
these processes are listed in Table 6.1.
Current limits from Table 6.1 date back to 2005 (1996 data) for BNL
experiments, and to 2011 for NA48/2 [4,14,60]. The sensitivity in NA62 is
expected to be of the order of
10−12
, and it should be possible to improve the

6.1 The necessity for a multi-ring algorithm 81
K+decay
mode
SM
violation
Branching ratio
at 90% C.L. Experiment
π+µ+e−LF <1.3×10−11 BNL E777 – E865
π+µ−e+LF <5.2×10−10 BNL E865 – CERN NA48/2
π−µ+e+L<5.0×10−10 BNL E865 – CERN NA48/2
π−e+e+L<6.4×10−10 BNL E865 – CERN NA48/2
π−µ+µ+L<1.1×10−9CERN NA48/2
Table 6.1:
Lepton Number (L) and Lepton Flavour Number (LF) violating
K+
decay modes
current branching ratio limits by at least one order of magnitude. Moreover,
NA62 will be equipped with better spectrometers compared to the previous
generation kaon experiments, providing a better mass resolution and allow-
ing cleaner separation between background events such as
K+→π+π+π−
and the signal region. This will allow direct searches in regions with low
expected Physics background.
LF violating decays may be pursued by NA62 to sensitivities correspond-
ing to possible tree-level contribution of new particles, where the decay
mode suppression arises from the mass of the exchanged field. A precise
measurement would rule out a fraction of theories providing LFV.
The detection of a lepton pair would result in a trigger opportunity for
such forbidden decay modes: allowed decays with more than one lepton
in the final state are highly suppressed, and always imply the presence of
a neutrino. As a consequence, they can be identified and discarded by the
analysis of the missing energy. The probability of misidentifying a pion
as a lepton is low, due to the presence of several P.ID.
1
detectors. The
high-resolution NA62 spectrometer makes it possible to apply stringent cuts
on the decay vertex, and to remove the background due to the pile-up of
different decay events.
For all these reasons, a real-time algorithm capable of fitting multiple
rings would be valuable.
Since no seedless multiple-ring-fitting algorithm exists, we chose to split
the problem in a preliminary “pattern recognition” step, needed to divide
the data set into single-ring candidates, and a subsequent
single-ring fitting
1Particle Identification.
82 “Ptolemy”, a two-step algorithm
Figure 6.1:
Ptolemy’s theorem is a relation among the lengths of the sides and those of the
diagonals in a cyclic quadrilateral.
stage.
6.2 Ptolemy’s theorem
For the pattern recognition step we chose to exploit Ptolemy’s trigonometric
theorem [27] about quadrilaterals inscribed in a circle, as first proposed by
G. Lamanna [43]:
Ptolemy’s Theorem.
For a cyclic quadrilateral, the sum of the products of the
two pairs of opposite sides equals the product of the diagonals.
For our application this theorem translates to the subsequent formula
(refer to Figure 6.1 for vertices and segments naming):
AB ·CD +AD ·BC −AC ·BD = 0 (6.1)
Given the coordinates of three points on a circle, we use this theorem to
check whether a fourth point belongs to the same circle or not. If it belongs
to the same circle, it is added into an array that contains the set of points
belonging to the given ring candidate.
Ideally, this process would be repeated until there are no points left, and
then the ring candidates would be fed to a ring-fitting algorithm that would
find the best centre and radius.

6.3 Reparametrization of the photomultipliers lattice 83
Unfortunately, our algorithm needs to be seedless, meaning that we do
not know a priori how many rings the current event contains, and we are
unable to identify three starting points belonging to the same ring. We must
therefore find an approximate way to define adequate starting “triplets” of
hits that will be fed to the Ptolemy algorithm.
In this chapter I will examine the building blocks of the trigger algorithm
developed for this project. In Section 6.4 I will examine the procedure de-
vised for the definition of four initial suitable triplets in detail. However, we
first need to go through a short description of the data fed to the procedure
(Section 6.3). Chapter 7will describe the GPU implementation of the whole
trigger program more thoroughly.
6.3 Reparametrization of the photomultipliers
lattice
The test setup and the data format used to send data to the GPU will be
described in Chapter 7.2.1.
In order to store
x
and
y
coordinates in 8-
bit
words, as demanded by the
data format described in Figure 7.4, we reparametrized the frame enclosing
the RICH focal plane in a way that is computationally efficient. Each of
the two round flanges hosts 976 photomultipliers distributed on a compact
hexagonal lattice (see Figure 6.2). We have assigned a progressive integer to
each
x
-axis point occupied by a vertex of the lattice, and another progressive
integer to each
y
position. As a result, we are effectively defining a lattice
where half of the vertices are occupied by the centre of a photomultiplier;
this way, a 38
×
66 lattice is enough to contain all the readout devices of a
flange, whose coordinates can therefore be represented by two 8-
bit
integers.
The two flanges are equal and will be superimposed in the process of ring
fitting, therefore only one 38
×
66 lattice is needed. Figure 6.3 shows a
reparametrized RICH flange.
Coordinate reparametrization is operated through the following formu-
las:
x(x) = round nx
x−xmin
xmax −xmin (6.2)
84 “Ptolemy”, a two-step algorithm
Figure 6.2:
Hexagonal packing of circles. Circle centres are spaced by
∆x= 1/2
in
x
, and
by
∆y=√3/2
in
y
. If
∆x
and
∆y
represent the gaps in a lattice, half of the lattice points
can host the centre of a circle [61].
y(y) = √3·round ny
y−ymin
ymax −ymin (6.3)
with
xmin = 0
xmax = 66
ymin = 0
ymax = 38
so that the centre of each PM, residing in
(x, y)
in the laboratory frame, is
represented by a
(x, y)
pair in the reparametrized frame. The roundings
are used to ensure that the output is the closest integer, rather than using
truncations. The vertical coordinates are inflated by a factor
√3
in order to
account for the asymmetrical filling factors of a compact hexagonal lattice.

6.3 Reparametrization of the photomultipliers lattice 85
0 10 20 30 40 50 60 70
0
10
20
30
40
50
60
70
RICH flange PM map for GPU trigger
0 10 20 30 40 50 60 70
0
10
20
30
40
50
60
70
Rescaled RICH flange PM map for GPU trigger
Figure 6.3:
Representation of the reparametrized RICH photomultiplier-holding flange.
The first frame shows the new PMTs coordinates, while the second one shows the lattice
that is used for GPU operations: vertical distances are increased by a factor
√3
because of
the filling characteristics of the compact hexagonal lattice.
The transformation can be inverted, obtaining:
x(x) = xmin +xmax −xmin
nx
x(6.4)
y(y) = ymin +ymax −ymin
√3ny
y(6.5)
The above conversion formulas prove useful to cast the results back in the
laboratory frame. If the program will return the coordinates
(a, b)
of the
centre and the radius
r
for each ring, the true values for these parameters
can be obtained simply by computing
a=x(a)(6.6)
b=y(b)(6.7)
r=xmax −xmin
nx
r(6.8)
The last formula is obtained making use of the equivalence between the
two factors
xmax −xmin
nxymax −ymin
√3ny9(6.9)

86 “Ptolemy”, a two-step algorithm
(up to the small rounding needed to cast the laboratory coordinates as the
closest integers), that describes the scaling between rescaled and laboratory
coordinates, and computing the distance between the centre and one point
of the circle:
x=a+rcos θ
y=b+rsin θθ≡0
−−−−−−→ x
0≡a+r
y
0≡b(6.10)
Here
θ
is an arbitrary phase, that we set to 0 for simplicity. This point
corresponds, in the laboratory frame, to the point
(x(a+r), y (b))
. The
distance to the centre will then be:
r2= [x(a)−x(a+r)]2+ [y(b)−y(b)]2(6.11)
= [x(a)−x(a+r)]2(6.12)
r=x(a)−x(a+r)=xmax −xmin
nx
r(6.13)
6.4 Pattern recognition
A convenient way must be found to initialize the process of checking the
data points through the Ptolemy’s theorem by providing sets of hit triplets.
The points assigned to each triplet should:
•
be well separated, in order to optimize the subsequent selection of hits
satisfying the Ptolemy’s theorem;
•
maximise in some way the probability of belonging to the same circle,
which would result in a better capability of identifying the maximum
number of ˇ
Cerenkov rings.
All the possible triplets of points would have to be tried in order to max-
imise the efficiency of the pattern recognition step. However, this approach
is extremely time expensive and therefore not feasible at an online level
within a maximum latency of 1
ms
. It is also unclear whether this approach
would work even in an offline approach, as the amount of memory needed
to store all those subsets of data could be higher than what is available on
certain GPU devices. For example, for a 20-hit event, there are 1140 possible
triplets. This means that, for each event, 6.84
kB
of memory are needed
only to store the 16
bit
indexes of the hits forming the triplets. Supposing
half of the triplets match a 20-hit ring, 1.49
GB
of data would need to be
stored and processed per batch of processed events (see Chapter 7). The
NVIDIA Tesla K20 GPU used for this work, that is quite a state-of-the-art

6.4 Pattern recognition 87
device, features 5
GB
of global memory in total (see Chapter 7.1), but “only”
369 MB per multiprocessor, i.e. available at the same time.
On the other hand, the fastest approach would consist in choosing three
points at random. Again, this procedure would not be optimal, as the ring-
detection efficiency would be low.
A procedure is needed, according to which the triplets of points should
be selected. Looking at some events from a
K+→π+π0
sample, we may
notice that, on a statistical basis, except for events with hits caused by noise
or by particles from the beam halo, the ˇ
Cerenkov rings are rarely concentric
or close to each other. A feasible approach may therefore consist in selecting
the “border” hits, as there is a high chance that they belong to the same
circle. Figure 6.4 shows two typical π+π0events.
We chose to select:
•the leftmost three points (XMIN triplet)
•the rightmost three points (XMAX triplet)
•the three points at the bottom of the frame (YMIN triplet)
•the three points on top of the frame (YMAX triplet)
with the following condition on the distance
d
between the points
ti
,
tj
belonging to the same triplet:
d2
ti,
tj> d2
th (6.14)
where the minimum square distance was set to
d2
th = 8
(in the rescaled
units) after empirical tests: greater threshold distances do not increment the
identification efficiency of ring candidates, and they increase the probability
of selecting hits belonging to different ˇ
Cerenkov rings.
The choice of triplets for the two-rings event shown in Figure 6.4(b) is
illustrated in Figure 6.4(c).
The maximum number of rings that can be detected in this way is four.
The NA62 experiment does not focus on the study of events with more than
one charged particle, anyway. In fact, the result we need to achieve at this
stage is an efficient detection of at least one circle, possibly in presence of
other hits or parts of additional rings.
Events featuring less than 5 or more than 32 hits were discarded for
this study, whose aim is in fact to strengthen the
π+π0
rejection achieved

88 “Ptolemy”, a two-step algorithm
x [mm]
-300 -200 -100 0 100 200 300
y [mm]
-300
-200
-100
0
100
200
300
+
πA RICH event featuring a
(a) One-ring event
x [mm]
-300 -200 -100 0 100 200 300
y [mm]
-300
-200
-100
0
100
200
300
+
and an e
+
πRICH event featuring a
(b) Two-ring event
(c) Two-ring event: pattern recognition
Figure 6.4:
Two typical
π+π0
events as detected by the RICH subdetector. In the event
represented in the top left panel, only a
π+
was detected. On the top right panel we see
two rings, one of which arose from a
π0
Dalitz decay: a positron from
π0→e+e−γ
was
detected as well. Finally, the bottom panel demonstrates the initialization of a pattern
recognition procedure. Starting from each side of the frame, the outermost three hits
are selected, which undergo a condition of reciprocal distance greater than a minimum
threshold. Each point can be chosen to belong to more than one “triplet”.

6.5 Single-ring fit 89
N. of events
2000 4000 6000 8000 10000 12000 14000 16000
s)µComputing time per ring (
-2
10
-1
10
1
10
2
10 POMH
DOMH
HOUGH
TRIPL
MATH
Figure 6.5:
Kernel execution time per single-ring event (20 hits) as a function of the
number of events processed in one batch on a NVIDIA Tesla C1060 GPU [26].
at the standard L0 trigger level. The upper limit condition may be dropped
in order to develop a positive trigger for multi-particle events, such as the
lepton number or lepton family number violating channels
K+→π−µ+µ+
(B.R.
<3·10−9
) or
K+→π+µ−e+
(B.R.
<5·10−10
); in this case, however,
more GPU threads should be allocated for each triplet, allowing for a higher
number of hits, and therefore fewer events could be processed simultane-
ously.
6.5 Single-ring fit
For the ring fitting stage, several single-ring fitting algorithms were previ-
ously examined in [26]. Five non-iterative procedures were implemented
and tested using Montecarlo generated data with rings of variable position,
radius and number of hits.
Two of the tested algorithms, nicknamed “POMH” (Problem-Optimized
Multi-Histograms) and “DOMH” (Device-Optimized Multi-Histograms), em-

90 “Ptolemy”, a two-step algorithm
ployed parallelization at the algorithm level only, with approximately 1000
GPU cores being used concurrently to process a single event.
Another tested algorithm (“HOUGH”) was based on a series of Hough
Transforms
2
and reduced the problem to that of finding intersections be-
tween circles centred on each hit photomultiplier.
A geometrical approach was examined with the “TRIPL” algorithm, for
which the centre is determined by the intersection of the mid-points axes of
pairs of segments defined by randomly chosen triplets of hits. In order to
achieve a good resolution and to gain robustness against the noise, several
triplets had to be used for each event, averaging the results.
Finally, a simple approach was tested, which used a least square method
to identify the best circle parameters (“MATH”). In this case, parallelization
was exploited only by processing several events at the same time.
The best results in terms of fit accuracy and execution time per event,
shown in Figure 6.5, were obtained with this last algorithm, suggesting that
simple geometrical or algebraic approaches are most advisable in a context
where reliability of results is a key issue.
For the above reason, I examined a number of algebraic ring fitting
methods, mostly described in [24], in order to select the best one in terms
of robustness and execution time. A procedure devised by Gabriel Taubin in
1991 [66] turns out to be the most computationally safe algorithm, being
also quite robust with respect to noise that could affect the estimation of
the radius, which “MATH” is not. A mathematical description of the “MATH”
and Taubin algorithms is available in Appendix A.
I implemented both procedures in a simple test framework and measured
their execution times, in order to check if the Taubin algorithm could be
used in our kernel in place of MATH. The two kernels were executed on a
Nvidia Tesla K20 GPU with an increasing number of single-ring events per
execution batch. The result, shown in Figure 6.6, highlights the negligible
time difference between the two. As a consequence, we could safely decide
to adopt the Taubin algorithm to perform the single-ring fitting part of our
program.
2
The Hough Transform is a pattern extraction technique aimed at finding instances of
objects of a certain shape in a noisy environment, by means of a voting procedure.
6.5 Single-ring fit 91
Events per packet
1 10 2
10 3
10 4
10
s)µ
Execution time per event (
0.01
0.02
0.1
0.2
1
2
10
20
30
Taubin
Math
Algorithm execution time on Tesla K20c
gcc 4.6.3-2 (Red Hat)
CUDA release 5.0
Figure 6.6:
Execution times of the MATH and Taubin kernels as a function of the number
of events processed in one batch on a NVIDIA Tesla K20c GPU.

7
Implementation on GPUs
Contents
7.1 GPU architecture and CUDA framework ......... 93
7.1.1 CUDA memory hierarchy .............. 96
7.1.2 Streams and concurrency .............. 96
7.2 Multi-ring algorithm implementation .......... 97
7.2.1 Test framework, data format and input ....... 97
7.2.2 Data stream flow and triplet forming ........ 99
7.2.3 Implementation of the kernel ............104
7.2.4 Implementation of the trigger ............105
7.1 GPU architecture and CUDA framework
Originally designed for the video-game market and the handling of screen
graphics, GPUs are massively parallel multiprocessors equipped with large
fast access on-board memory. Unlike CPUs, much more silicon area is
devoted to computing units than to control structures (Figure 7.1). The
computing power of GPUs arises from the large number of processing cores
installed on the device, rather than from the chip clock speed (as for CPUs).
Graphic card devices are indeed used to execute highly parallelized tasks.

94 Implementation on GPUs
CACHE
ALU
CONTROL
ALU
ALU
ALU
DRAM
CPU
DRAM
GPU
Figure 7.1:
Compared to the CPU, the GPU devotes more transistors to data processing
[53].
The trigger algorithm and the test framework I will describe in Sec-
tion 7.2.1 use the CUDA (Compute Unified Device Architecture) toolkit
1
.
CUDA is a platform for parallel programming and computing developed
by NVIDIA
2
, compatible with GeForce, Quadro and Tesla GPUs. This plat-
form exposes GPUs for computing just like any usual processor, through
CUDA-accelerated libraries and extensions to the most popular program-
ming languages.
A set of C/C
++
libraries enables heterogeneous programming and pro-
vides straightforward APIs
3
for device and memory management. GPUs
can be embedded in the PC motherboard, or on the CPU die, or reside in
dedicated graphics cards connected to the host PC via PCI Express links, as
in this work. Hereinafter, I will call host the CPU and its memory, and device
the GPU. Serial functions, decorated with the prefix, are coded in
standard C and execute on the processor; the host can call a
function (kernel) at any moment, that will run on the GPU.
A few definitions should be given before discussing the GPU architecture:
Thread: the smallest sequence of instruction that can be run independently.
Warp:
the minimum work group size, i.e. the maximum number of threads
that can execute the same instruction simultaneously, in SIMD mode
(Single Instruction – Multiple Data), within a single CUDA multiproces-
sor. Currently, all NVIDIA GPUs feature warps of 32 threads.
1
2
3Application Programming Interface

7.1 GPU architecture and CUDA framework 95
Figure 7.2:
Concurrent execution of thread blocks on devices with a different number of
multiprocessors: 2 SMs (left) and 4 SMs (right) [64].
Block:
the basic element of a GPU program. The threads of a block execute
concurrently on one multiprocessor, and multiple blocks can run at
the same time. New blocks are launched on the free multiprocessors,
as the previous ones terminate.
The building block of the GPU architecture is the Streaming Multipro-
cessor (SM), which hosts a number of single-precision CUDA cores (see
Appendix C) executing identical sets of instructions, and a block of high-
speed on-chip memory. Up to 24 warps can be active at the same time
on a single SM, depending on their memory usage and on the number of
registers available on the SM. Each block of threads can be scheduled in any
order on any of the available SMs, allowing for program scalability: devices
with more SMs automatically outperform older GPUs, as demonstrated in
Figure 7.2 [53]. One of the most important characteristics of the CUDA ar-
chitecture, indeed, is that kernels are scalable across any number of parallel
SMs to adapt to different hardware.
The CUDA runtime manages the number of blocks processed simultane-
ously by the GPU SMs, that is closely linked to the availability of hardware
resources.
A kernel is launched with a call
where:
•
the triple angle brackets denote a call to a device function by a host
function;

96 Implementation on GPUs
•
the kernel is only executed by the stream (see Section 7.1.2);
•
the input parameters point to the device memory, that must be allo-
cated before the kernel call;
•
is executed at the same time by a grid of
independent blocks;
•
each block is split into threads that can synchronize
and communicate to each other through access to the shared memory;
•
a portion of shared memory (see Section 7.1.1) of size
is allocated for each block.
The same kernel is executed by all the threads. Data-parallel program-
ming maps data elements to parallel processing threads: inside the kernel
function, jobs can be distributed to the blocks and split between the threads
of a block by means of the built-in three-dimensional indices and
. This provides a natural way to invoke computation across the
elements of a multidimensional domain, such as matrices and vectors [53].
Individual threads executing in a warp are free to execute independently via
data-dependent conditionals branches. In this case, all the branched paths
are scheduled serially. Threads can be synchronized, i.e. can execute a com-
mon instruction at the same time, through dedicated CUDA functions, and
automatically synchronize upon convergence to the same instruction branch.
7.1.1 CUDA memory hierarchy
The CUDA architecture features a hierarchy of memory spaces that are
accessible in different scopes. All threads have read/write access to a large
memory space called global (some
GB
), persistent across subsequent kernel
launches within the same application. A different space, residing on each
Streaming Multiprocessor, is devoted to independent portions of memory –
referred to as shared memory – visible to all the threads of the same block.
The lifetime of the shared memory coincides with the execution time of the
block. Finally, each thread has access to a small private local memory space
[53].
7.1.2 Streams and concurrency
Since the development of the Fermi
4
architecture, NVIDIA GPUs can execute
up to three streams at the same time, allowing to concurrently manage
4

7.2 Multi-ring algorithm implementation 97
K2
HD3
K1
K3
K4
HD1 DH1
DH2
DH3
DH4
HD2
HD4
Figure 7.3:
3-way concurrency demonstrated for a four-step program [57]. At the beginning,
data is copied from the host memory into the device memory (HD). As the copy is executed,
the stream is free to undertake another operation. At the second step, one stream executes
the kernel (K), and another one concurrently copies more data into the device memory. At
the following step, as soon as the previous two operations are concluded, three streams can
run at the same time: the first one pulls the results of the previous execution of the kernel
from the device, and stores them back into the host memory (DH); the second executes the
kernel on the last data copied into the device memory; the third pushes some more data
into the device memory.
processing and data transfers between host and GPU of different data sets.
A
CUDA stream
is a sequence of operations that execute in issue-order
on the GPU [57]. CUDA operations from different streams may run con-
currently and be interleaved. As an example, the concurrent execution of
a small kernel in up to four streams may use as much as possible of the
GPU computing resources at once. The maximum number of kernels that a
device can run at the same time is four [69].
A typical example of concurrent execution of streams emerges from the
possible overlapping of host to device and device to host memory copies and
of the execution of a device kernel. We have adopted this solution, often
referred to as “3-way concurrency”, for this project. Figure 7.3 explains the
concurrent execution of such three streams.
7.2 Multi-ring algorithm implementation
7.2.1 Test framework, data format and input
A framework was built by F. Pantaleo [55], that consists of a multi-threaded
software platform designed in order to optimize the execution latency of
a given set of instructions. The platform executes on the CPU as host for
GPU-based applications.
The main components are four:

98 Implementation on GPUs
•Network communication manager
•Process scheduler
•Device kernel (on the GPU)
•Trigger monitor
Network communication is handled by means of a modified API for the
“Direct NIC Access” (DNA) driver
5
. This driver represents an alternative to
the usual ethernet drivers, and it exposes the memory buffers stored on the
Network Interface Controller (NIC) board to the user space. This way, data
can be accessed directly from the NIC buffers, without the need of copying
them to the host RAM first: this results in a lower and much more stable
latency.
This part of the framework allows the user to use a large number of
network interfaces. A thread is spawned for each interface, to handle the
network communication.
The framework includes a scheduler in charge of handling a smart
queue, managing multiple “producer” and asynchronous “consumer” pro-
cesses. Data produced by threads running the network communication is
accumulated in host memory buffers. Each buffer is copied to the device
memory only when a predefined size is reached or when a “timeout” flag is
raised: in order to sustain the throughput, the host waits for a good number
of MTP packets within a given maximum time window. After that, the GPU
kernel (where the trigger algorithm resides) is executed, and the results
are copied back to the host memory. The full pipeline is managed by three
independent software threads.
Finally, information about the status of the network communication
and, possibly, real-time trigger results are displayed by a monitor refreshing
every 5
s
. The data shown include the number of UDP
6
packets read from
each interface, the saturation of the network links and the number of MTPs
processed by the GPU.
The firmware of the readout system for NA62 is still under development.
For the tests reported in Chapter 8we assumed that the TEL62 boards read-
ing out the signals from the photomultipliers of the RICH will also take care
of the conversion between the PMT channel IDs and their 8-
bit
coordinates.
A simple look-up table will be implemented for this purpose on the board
5
6User Datagram Protocol

7.2 Multi-ring algorithm implementation 99
firmware.
I customized the Montecarlo simulation and event reconstruction frame-
work provided by NA62 to prepare six different sets of data:
•K+→π+ν¯νevents selected with the standard signal and L0 cuts;
•K+→π+ν¯ν
events selected with the standard signal cuts and relaxed
hit multiplicity 5≤n≤64 on the RICH;
•K+→π+π0events selected with the standard L0 cuts;
•K+→π+π0events with hit multiplicity 5≤n≤64 on the RICH;
•K+→π+π+π−events selected with the standard L0 cuts;
•K+→π+π+π−events with hit multiplicity 5≤n≤64 on the RICH.
Each data set was divided in files containing 256 events each.
In addition, we supposed that the geometric correction related to the tilts
of the RICH mirrors (Eqn. 4.1) would also be computed by the TEL62 boards,
before data are sent to the GPU. As a consequence, the lattice introduced in
Section 6.3 had to be modified in order to avoid the repositioning of hits on
“phantom” lattice vertices with negative
x
coordinates. Therefore, the whole
frame was shifted by 85 units towards the positive side of the
x
axis, i.e. the
8-bit coordinates were computed as
x(x) = round nx
x−xmin
xmax −xmin + 85 (7.1)
instead of using Eqns. 6.2 and 6.3.
The UDP packets sent to the PC by the TEL62 boards contain all the
relevant data we need for the analysis. Each packet consists of a header
and a data container with the structure shown in Figure 7.4. These data are
prepared by the TEL62 boards as UDP packets and sent to the NIC.
7.2.2 Data stream flow and triplet forming
It is convenient to define some constants before going through the imple-
mentation of the algorithm:
Here, represents the maximum number of hits allowed per event.
This value was initially set to 32 in order to analyse events that have

100 Implementation on GPUs
Source ID Format Reserved
Source sub-ID Num. of events Total MGP length
Event data
Event data
. . .
Event timestamp
Reserved
Hit ID y Hit ID x Hit ID y Hit ID x
Hit ID y Hit ID x Hit ID y Hit ID x
Event fine time Number of hits
. . .. . .
Bits 31 16 15 0
Figure 7.4:
Structure of the data files produced by the TEL62 boards. The top panel shows
a GPU multi-trigger primitive packet. The bottom panel shows how data are packed for
each event.
already passed the standard online selection
7
. Input from the NIC board is
continuously read; the number of events packed in a UDP packet is read
from the UDP header. Event data is written into structures, defined
below, that are copied to the local memory of the GPU when a predefined
size ( ) or data accumulation time has been reached. I will discuss
the choice of =256 in Chapter 8.3.
In particular, the and arrays are filled with the coordinates of
all the events of the batch, i.e. of the set of events processed
concurrently:
x[]=x0x1x2··· x31
evt 0
x32 ··· x63
evt 1
x64 ··· (7.2)
y[]=y0y1y2··· y31
evt 0
y32 ··· y63
evt 1
y64 ··· (7.3)
The data format is fixed and independent from the actual hit multiplicity: if
an event counts less than hits, some locations are left empty. Let us
7
In Chapter 8I will also test the possibility of increasing (actually doubling) this
limit: if the GPU-based trigger proves efficient enough in the high-multiplicity region, the
multiplicity cut could be eliminated from the hardware L0 trigger.

7.2 Multi-ring algorithm implementation 101
also define an array of indices that will be used later:
I[ ] = 0 1 2 ··· 31
evt 0
32 ··· 63
evt 1
64 ··· (7.4)
This way, the
x
and
y
coordinates of the
n
-th hit in the scope of the current
event can be accessed through the same index:
xn=xI[n]
, and similarly
yn=yI[n].
While the 8-
bit
coordinates of hit PMTs are read and stored in and
arrays, the host program also checks if hits can be assigned to a triplet. For
each event, in fact, a array is defined, that hosts the indices of
the hits selected for the initialisation of the pattern recognition step:
triplet[]=t0t1t2
XMAX
t3t4t5
XMIN
t6t7t8
YMIN
t9t10 t11
YMAX
(∀event)(7.5)
The first element of the array is initialised with the index of the
first hit. The indexes of those subsequent hits whose coordinates satisfy the
conditions discussed in Section 6.4 are then written into the other elements.
As an example, the following code shows how the portion of the triplet
is populated.

102 Implementation on GPUs
Similarly, , and portions are populated. We obtain a 12-
elements array {tn}such that:
x[t0]≤x[t1]≤x[t2]≤x[t3]≤x[t4]≤x[t5](7.6)
y[t6]≤y[t7]≤y[t8]≤y[t9]≤y[t10]≤y[t11](7.7)
These operations are carried out once per event. The indices used in the
above code only fit the first event of the stream, while for the subsequent
events the triplet index is transformed as
tn−→ tn+ 12k
, where
k
is the
event index. The array containing triplets will then have the form
triplet[]=t0··· t11
evt 0
t12 ··· t23
evt 1
t24 ··· (7.8)
The operations described so far are executed on an event-by-event basis
by the host program, running on the CPU, while event data are read from the
NIC memory. This way, the population of the array is interlaced
with the readout and accumulation of UDP packets, so that smaller sets of
instructions need to be processed by the GPU cores.
When the event batch is ready, data is copied to the global memory of
the GPU, where the kernel is executed, and the results are copied back to
the host memory by means of dedicated CUDA functions:

7.2 Multi-ring algorithm implementation 103
where refers to the running stream, is a pointer to
an of data stored in the global memory, points to
the global memory allocated for the structure, and provides
temporary storage in a structure for variables that need to be
accessed while executing the circle fitting function:
In the above code, and are the hit coordinates relative to the hits center
of gravity frame; the other variables are polynomial combinations
of these two, that are used to compute the best ring parameters (see Ap-
pendix Bfor the actual CUDA implementation of the ring fit).
The kernel call parameters are defined as
so that 4 blocks execute for each event, each one handling a pattern recog-
nition stage initialised with a different triplet, and the corresponding single

104 Implementation on GPUs
ring fitting stage. Each block contains a number of threads equal to the
maximum number of hits per event. Finally, events are evaluated
concurrently. The amount of shared memory that has to be allocated will be
discussed later.
7.2.3 Implementation of the kernel
The kernel consists of 3 main subsets of instructions.
1.
An array containing the integer
x
and
y
coordinates of the hits forming
the current triplet (of dimension ) is created in the
shared memory, visible to all the threads of the block.
2. Each thread evaluates the Ptolemy’s theorem on a different hit of the
event, and if it stands it copies the hit coordinates to the
structure. A counter, stored in the shared memory ( ),
is incremented every time a hit is accepted by this pattern recognition
procedure.
3.
A semi-parallelized version of the Taubin ring fit algorithm, discussed
in Appendix A, is executed, and the structure is populated.

7.2 Multi-ring algorithm implementation 105
The code implementing the function is available in Appendix B.
This function finds the parameters of the best fitting circle in the reparame-
trized frame introduced in Section 6.3, also reverting the arbitrary 85-units
shift applied to Montecarlo-generated data (see Eqn. 7.1). The results are
then converted back to the laboratory frame.
Several arrays need to be reduced
8
: to achieve this, a modified version of
the function provided by the CUDA Data Parallel Primitives
Library (CUDPP)
9
is used, that allows to compute the sum of an array in
a small number of steps, as sketched and explained in Figure 7.5. All the
threads of the block participate to the reduction, and therefore a portion of
shared memory of size is allocated.
Both the kernel and the triplet finding procedures have been designed
together with F. Pantaleo.
7.2.4 Implementation of the trigger
After the execution of the kernel, results are copied back to the host memory
and made accessible to the user. A selective trigger program has been de-
8
Those array operations that return a result with a smaller rank are referred to as
“reductions”. In this case, the sum of the array elements is computed (rank 0), in order to
find their average.
9
106 Implementation on GPUs
Figure 7.5:
Parallel reduction of arrays within a single thread block [33]. The algorithm
recursively reduces the output size, by computing the local sum of 2 array elements.
Results are stored in the shared memory, visible to all the threads. A sequential addressing
approach is used for memory access, in order to prevent memory bank conflicts. This way,
the complexity of the algorithm is O(log2N)where Nis the size of the array.
veloped, that makes use of the ring fit results to perform basic kinematical
analysis on the events.
Four conditions are set to check the quality of the identified rings:
•
the radius belongs to a reasonable interval of values:
Rmin < R < Rmax
•
the number of hits on which a single-ring fit was executed exceeds a
minimum threshold: n>nth
•
the fraction of hits assigned to the ring candidate, compared to the
total number of hits in the event, exceeds a minimum threshold:
n/nhit > fth
•
the rings differ from each other:
|Ri−Rj|>∆Rth
and the distance
dij between the centres is dij > Dth .
where:
Rmin = 50 cm (7.9)
Rmax = 350 cm (7.10)
nth = 5 (7.11)
fth = 1/3(7.12)

7.2 Multi-ring algorithm implementation 107
∆Rth = 1 cm (7.13)
Dth = 2 cm (7.14)
These numbers have been optimised in order to minimise the number of
times signal events are erroneously rejected, while keeping the efficiency of
the trigger as high as possible.
Rings that do not satisfy the above condition are discarded and not used
to produce trigger decisions. The default behaviour is to produce a positive
decision, i.e. the current event is forwarded to the next trigger levels unless
some conditions, described below, are satisfied. For each event, if at least a
“good” ring is identified, a negative trigger decision is produced if one of the
following conditions holds:
•
at least two different rings are detected, and the following conditions
are satisfied:
–
the number of hits in the event is compatible with the presence of
more than one charged particle:
nhit >16 + nth ·(NR−1)
, where
nhit
is the number of hits of the event and
NR
is the number of
different rings found;
–
the rings were found using different hits:
NR
i=1 ni<1.3·nhit
(a
30% tolerance is introduced to account for partial rings overlap-
ping).
•
at least one ring is detected whose radius exceeds
Rth = 179 mm
,
according to the simulation results reported in Chapter 5;
•
at least one ring is detected, corresponding to a reconstructed kine-
matics such that δ > 0.002
where Rth and δare the cut variables introduced in Chapter 5.
If none of the above conditions is satisfied, a positive trigger decision is
produced.

8
Tests and conclusions
Contents
8.1 Trigger efficiency ...................... 109
8.2 Timing tests ......................... 115
8.3 Possible improvements and outlook ........... 119
8.4 Conclusions ......................... 121
8.1 Trigger efficiency
A total of 5120 Montecarlo-generated background events and 1536 signal
events from different samples were fed to the test framework. The number
of times the algorithm successfully identified and rejected a background
event is shown in Table 8.1. The efficiency for the signal was also computed
and it is shown in the same table. The errors shown represent pure statistical
uncertainties.
The trigger was run on two series of Montecarlo-generated data sets.
One series consisted of events that had passed the standard L0 selection (see
Chapter 3.2). This means that the multiplicity of hit PMTs was constrained
between 5 and 32. The other series was not filtered through the L0 trigger
requirements, but it was requested that each event had a number of hits
comprised between 5 and 64. The latter events were analysed in order to
explore the possibility of running a GPU-based trigger in parallel to a less
biased hardware trigger, where the RICH hit multiplicity cut is relaxed or
completely dropped. This way it would be possible to design special triggers

110 Tests and conclusions
Data type Sample Discarded Trigger efficiency (%)
π+π0L0 selected 1280 800 62.5 ±1.4
π+π+π−L0 selected 1536 920 59.9 ±1.3
π+π05≤nhit ≤64 1024 618 60.4 ±1.5
π+π+π−5≤nhit ≤64 1280 936 73.1 ±1.2
π+ν¯νL0 + Signal cuts 768 38 95.1 ±0.8
π+ν¯νSignal cuts 768 38 95.1 ±0.8
Table 8.1:
GPU trigger performance. The first four rows show the achieved rejection level
for four different background samples. The last two rows show the
K+→π+ν¯ν
efficiency
achieved before and after a standard L0 selection is performed (the rejected events differ
in the two cases, even if the result is the same).
to explore additional Physics channels.
The data sets were further divided into subsets according to the number
of hits in each event, to analyse the behaviour of the algorithm with respect
to this variable. The performance of the trigger on the various subsets is
shown in Figures 8.1(a) to 8.1(e).
We can infer from Figure 8.1(a) that the rejection for L0 filtered
π+π0
events increases with the number of hits. In particular, the low rejection
ε10 = (40.5±3.4)%
shown for events with
5≤nhit ≤10
arises from the
difficulty of fitting a ring with so few points. The three following bins yield
increasing rejection levels of
ε16 = (58.5±2.6)%
,
ε23 = (69.4±2.0)%
and
ε32 = (76.0±3.1)%
, respectively: as the number of hits per event increases,
chances are that the fraction of spurious hits due to the presence of other
partial rings decreases. The identification of rings is therefore easier, with
the effect of increasing the rejection capability of the trigger (as discussed
in Section 7.2.4, events are rejected only if the quality of the identified rings
exceeds a threshold defined by a few parameters).
On the other hand, the initial low-multiplicity rejection capability achieved
for
3π
events with few hits is higher (plot 8.1(c)): in this case,
ε10 =
(49.3±3.1)%
. In fact, in this case it is more probable that at least one
ˇ
Cerenkov ring is present in the RICH detector. However, Figure 8.1(c)
highlights that for
3π
events there is no steep increase of rejection power
with the number of hits, as there is for the 2-body background. This is
probably due to the fact that the trigger is not optimized for the
π+π+π−
8.1 Trigger efficiency 111
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
10≤
hit
n≤5 16≤
hit
n≤11 23≤
hit
n≤17 32≤
hit
n≤24
rejection efficiency
0
π
+
π
(a)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
16≤
hit
n≤5 32≤
hit
n≤17 48≤
hit
n≤33 64≤
hit
n≤49
rejection efficiency
0
π
+
π
(b)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
10≤
hit
n≤5 16≤
hit
n≤11 23≤
hit
n≤17 32≤
hit
n≤24
rejection efficiency
-
π
+
π
+
π
(c)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
16≤
hit
n≤5 32≤
hit
n≤17 48≤
hit
n≤33 64≤
hit
n≤49
rejection efficiency
-
π
+
π
+
π
(d)
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
10≤
hit
n≤5 16≤
hit
n≤11 23≤
hit
n≤17 32≤
hit
n≤24
acceptanceνν
+
π
(e)
Figure 8.1:
Trigger rejection for
π+π0(a, b)
and
π+π+π−(c, d)
backgrounds, and signal
efficiency
(e)
. The distributions on the right differ from the ones on the left for the data set
used: on the left
(a, c)
, the trigger was run on Montecarlo-simulated events that passed
the standard L0 selection. On the right
(b, d)
, only a relaxed
5≤nhit ≤64
cut was applied
to the input data set. Standard L0 selection and signal cuts (see Table 5.1) were applied for
the πν¯νdata set shown in the bottom panel (e).

112 Tests and conclusions
background. As the number of hits increases, it is easier to detect a single
ring, but it becomes more difficult to separate an increasing number of
rings. In principle, this difficulty might be overcome by using more triplets
in the pattern recognition procedure. The trigger rejection computed in
the other three bins reads:
ε16 = (60.4±3.0)%
,
ε23 = (60.7±2.7)%
and
ε32 = (63.6±1.9)%.
Plots 8.1(b) and 8.1(d) display the level of background rejection achieved
on the second series of input data, that was selected with a relaxed multi-
plicity cut only (5≤nhit ≤64).
In particular, from Figure 8.1(b) we learn that most
π+π0
events can be
correctly identified, and therefore rejected, when the number of hits found
is greater than 32:
ε16 = (44.0±2.5)% (8.1)
ε32 = (64.3±2.1)% (8.2)
ε48 = (89.4±3.0)% (8.3)
ε64 = (92.3±4.3)% (8.4)
The level of event rate suppression achieved for the set of
π+π+π−
events
can be read from plot 8.1(d):
ε16 = (53.2±3.8)% (8.5)
ε32 = (68.6±2.0)% (8.6)
ε48 = (82.8±1.6)% (8.7)
ε64 = (93.8±6.1)% (8.8)
The trigger proves most powerful for high-multiplicity events: it could
be therefore feasible, in principle, to drop the RICH multiplicity cut from
the standard trigger, and to rely only on the GPU-based alternative.
The results plotted in Figure 8.1(e), finally, ensure that the design of this
algorithm is optimized to minimize unwanted suppression of the signal. The
plot shows the efficiency for
K+→π+ν¯ν
decays that passed the standard
L0 selections, for different intervals of hit multiplicity:
1−ε10 = (98.4±1.1)% (8.9)
1−ε16 = (94.7±1.2)% (8.10)
1−ε23 = (93.6±1.5)% (8.11)
1−ε32 = (97.2±2.7)% (8.12)

8.1 Trigger efficiency 113
A study of the signal efficiency carried out on a set of
π+ν¯ν
data not prelimi-
narily filtered by the standard L0 selections yielded the same global results
(Table 8.1). However, no
π+ν¯ν
events with hit multiplicity higher than 32
could be found after performing the signal selection described in Table 5.1.
It must be pointed out that none of the selections implemented in the
trigger (see Section 7.2.4) were designed specifically to cope with the
3π
background. The algorithm should be further optimized in order to suppress
the rate of these events. The tests reported in plots 8.1(b) and 8.1(d) were
only intended to verify, on events that may feature more than one ˇ
Cerenkov
ring, the efficiency of the ‘multi-ring’ algorithm I developed.
Plots 8.2(a) to 8.2(e) analyse the data sets used for the tests described
in this section. The multiplicity of hits in the events is shown as a function
of the number of different rings detected, for the data sets described above.
We can observe that:
•
The number of times no rings could be identified approaches zero,
for
π+π0
events, as the number of hits in the event grows, and in
particular for
nhit >32
. This explains why the trigger is more powerful
for high-multiplicity primitives.
•
While
π+π0
events mostly exhibit a single ˇ
Cerenkov ring, in a sig-
nificant fraction of the
3π
events analysed two rings were detected.
This fraction increases with the hit multiplicity up to approximately
nhit 35
, and then it decreases. This is a hint that the 4-triplets
approach used for this work cannot efficiently handle events with a
very large hit multiplicity.
•
The number of times three different rings were detected is very small.
However, it is not possible to state that this is due to a problem in the
algorithm discussed here. The current NA62 analysis software does
not provide any straightforward way to know the actual number of
ˇ
Cerenkov rings formed, or the actual number of charged particles that
crossed the RICH volume. Besides, in order to verify the real ring de-
tection efficiency, the format of data fed to the GPU should be modified
to include “Montecarlo-truth” information. A “toy” simulation with a
custom ring generating tool might be designed to perform these tests.
The algorithm I designed represents only a starting point for a real-time
application of GPUs in High Energy Physics. The results achieved with this
work can still be improved by devoting further effort to the development of
a parallelized trigger algorithm, and to the study of its performance.
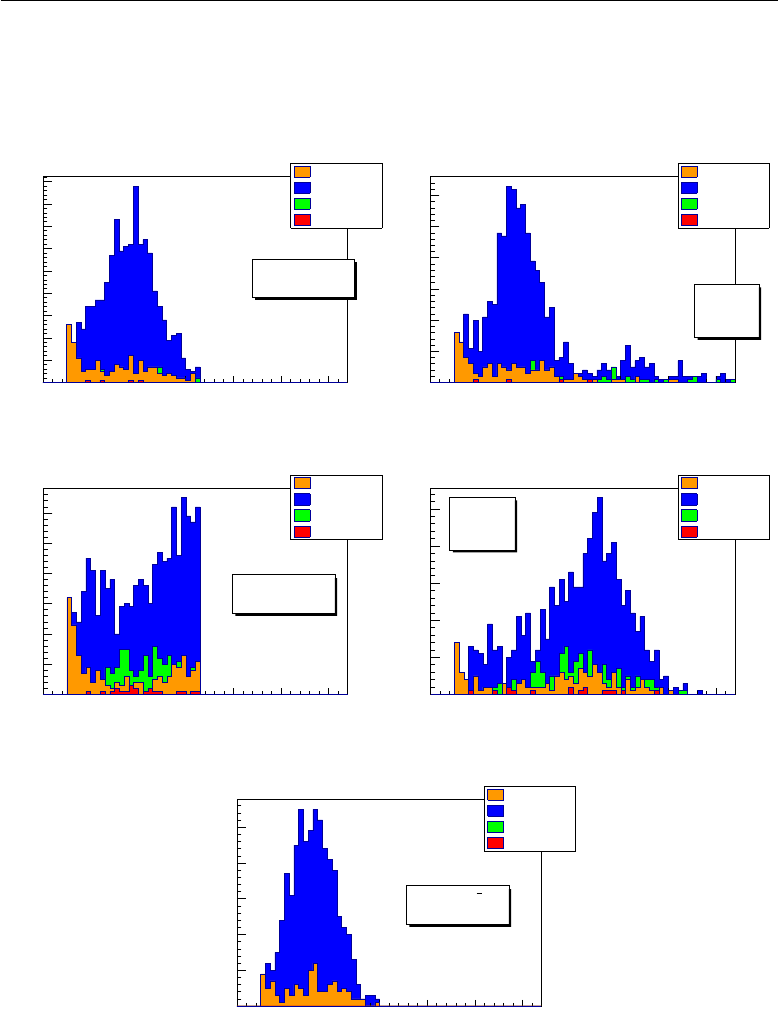
114 Tests and conclusions
h1ring
Entries 1027
Mean 17.59
RMS 5.68
Number of hits in events with N rings
0 10 20 30 40 50 60
0
10
20
30
40
50
60
70
80
90 h1ring
Entries 1027
Mean 17.59
RMS 5.68
h2rings
Entries 65
Mean 17.89
RMS 6.059
h0rings
Entries 184
Mean 14.23
RMS 7.528
h3rings
Entries 4
Mean 14.75
RMS 4.437
h4rings
Entries 0
Mean 0
RMS 0
0 rings
1 ring
2 rings
3 rings
0
π
+
π →
+
K
Standard L0 cuts
(a)
h1ring
Entries 823
Mean 21.06
RMS 10.55
Number of hits in events with N rings
0 10 20 30 40 50 60
0
10
20
30
40
50
60
h1ring
Entries 823
Mean 21.06
RMS 10.55
h2rings
Entries 58
Mean 30.26
RMS 13.43
h0rings
Entries 139
Mean 16.3
RMS 10.06
h3rings
Entries 4
Mean 21.25
RMS 9.337
h4rings
Entries 0
Mean 0
RMS 0
0 rings
1 ring
2 rings
3 rings
0
π
+
π →
+
K
64≤
hit
n≤5
(b)
h1ring
Entries 1089
Mean 20.75
RMS 7.981
Number of hits in events with N rings
0 10 20 30 40 50 60
0
10
20
30
40
50
60
h1ring
Entries 1089
Mean 20.75
RMS 7.981
h2rings
Entries 215
Mean 21.29
RMS 6.139
h0rings
Entries 211
Mean 16.4
RMS 9.93
h3rings
Entries 21
Mean 20.1
RMS 5.991
h4rings
Entries 0
Mean 0
RMS 0
0 rings
1 ring
2 rings
3 rings
-
π
+
π
+
π →
+
K
Standard L0 cuts
(c)
h1ring
Entries 930
Mean 30.25
RMS 10.16
Number of hits in events with N rings
0 10 20 30 40 50 60
0
10
20
30
40
50
h1ring
Entries 930
Mean 30.25
RMS 10.16
h2rings
Entries 189
Mean 30.16
RMS 9.474
h0rings
Entries 145
Mean 25.49
RMS 12.78
h3rings
Entries 16
Mean 27.62
RMS 10.82
h4rings
Entries 0
Mean 0
RMS 0
0 rings
1 ring
2 rings
3 rings
-
π
+
π
+
π →
+
K
64≤
hit
n≤5
(d)
h1ring
Entries 650
Mean 15.58
RMS 4.614
Number of hits in events with N rings
0 10 20 30 40 50 60
0
10
20
30
40
50
h1ring
Entries 650
Mean 15.58
RMS 4.614
h2rings
Entries 8
Mean 16.25
RMS 2.773
h0rings
Entries 110
Mean 14.73
RMS 5.998
h3rings
Entries 0
Mean 0
RMS 0
h4rings
Entries 0
Mean 0
RMS 0
0 rings
1 ring
2 rings
3 rings
νν
+
π →
+
K
Standard L0 cuts
(e)
Figure 8.2: Hit multiplicity in the triggered data sets.

8.2 Timing tests 115
8.2 Timing tests
The possibility of actually implementing a useful GPU trigger algorithm
ultimately depends on the possibility of running it at a high input rate, and
within a time lower than the predefined trigger latency.
Before analysing the real time performance of the trigger, it is useful
to remind that all GPU-related latencies depend on the specifications of
the device on which the program is compiled and executed. Appendix C
lists all the relevant features of the NVIDIA Tesla K20 GPU that was used
for the tests reported here. In particular, this device has a warp size of 32
threads. This means that, if we set a number of threads per block equal to
the maximum hit multiplicity, those data sets with hit multiplicity
nhit ≤32
will be processed with a single warp execution, while the
5≤nhit ≤64
data sets will require a queue of two warps for each triplet (triplets are
processed concurrently, thanks to the high number of available CUDA cores).
The histograms of Figure 8.3 report separately the three CUDA latencies
adding up to the total latency of the GPU trigger:
1.
the time
∆tH→D
needed to copy the data corresponding to a batch of
events into the global memory of the GPU;
2. the kernel execution time ∆tker nel;
3.
the time
∆tD→H
needed to copy the results back to the host user space
(an eventually to the TDAQ system).
The measurements were repeated 100 times, using the same L0-filtered
π+π0data set (256 events). The measured latencies are:
∆tH→D= 27 ±2µs (8.13)
∆tkernel = 196 ±2µs (8.14)
∆tD→H= 24 ±2µs (8.15)
summing up to a total latency ∆ttot (Figure 8.4(a))
∆ttot = 247 ±6µs (8.16)
and therefore to a total latency per event:
∆tevt = 0.97 ±0.02 µs (8.17)
since 256 events are processed per batch.
116 Tests and conclusions
h2d
Entries 100
Mean 0.02714
RMS 0.001909
Host to Device time [ms]
0.015 0.02 0.025 0.03 0.035 0.04 0.045
0
2
4
6
8
10
12
14
16
h2d
Entries 100
Mean 0.02714
RMS 0.001909
CUDA Host to Device copy
ker
Entries 100
Mean 0.1963
RMS 0.002008
Kernel execution time [ms]
0.17 0.18 0.19 0.2 0.21 0.22 0.23
0
5
10
15
20
25
ker
Entries 100
Mean 0.1963
RMS 0.002008
CUDA Kernel
d2h
Entries 100
Mean 0.02351
RMS 0.001738
Device to Host time [ms]
0.01 0.015 0.02 0.025 0.03 0.035 0.04
0
2
4
6
8
10
12
14
16
18
20
22 d2h
Entries 100
Mean 0.02351
RMS 0.001738
CUDA Device to Host copy
Figure 8.3:
GPU execution latencies for a batch of 256
π+π0
events preliminarily filtered
by the standard L0 selection. The measurement was repeated 100 times. The first panel
shows the time needed to copy the whole data set from the host RAM to the global memory
of the GPU. The second panel shows the kernel execution time. The last one shows the
time needed to copy the results back to the host.

8.2 Timing tests 117
These simulated events were preloaded in an internal emulation buffer
of the TEL62 TDAQ boards and sent from there to the NIC at 600
±
25
kHz
rate. Due to the limited buffer memory of the TEL62 board, it was not
possible to prepare large data files with more than 256 events; nor was
it possible to transmit different samples in a queue. Therefore, in order
to measure the time response stability of the trigger, we had to capture
1
a set of UDP packets (256 events) and transmit them in a loop from an
Ethernet interface to another one on the same PC, using the applica-
tion provided with the DNA driver APIs
2
. In the future, it will be useful to
test the framework with a continuous stream of real data from TEL62 boards.
Figure 8.4(b) reports the results of some time stability tests. The total
execution time was analysed using all the data sets discussed in Section 8.1.
Here, the total GPU latency is reported as a function of the number of the
processed batch: 100 batches = 25600 events were transmitted to the NIC
in a row, with event packets sent at a rate of 0.1
GB/s
, that corresponds to
about 0.7 to 5.6
MHz
event rate depending on the number of hits. These
results show that the GPU performs best when it is under full load, i.e. the
maximum execution speed is not reached for the first and last few execu-
tions. However, this should not be a problem if the trigger operates with a
stable particle beam.
From Figures 8.4(a) and 8.4(b) we can also infer that the plateau latency
of the trigger is not doubled when the number of threads per block is raised
from 32 to 64 (
5≤nhit ≤64
event sets). In fact, the total kernel execution
time results from the sum of two contributions: a kernel launch time, that is
fixed and not measurable, and the time needed to perform the operations
issued in the kernel function. For example, the total time needed to process
256 3πevents, with hit multiplicity 5≤nhit ≤64, amounts to
∆ttot = 271 ±5µs (8.18)
corresponding to
∆tevt = 1.06 ±0.02 µs (8.19)
per event, to be compared with the result reported above in Eqn. 8.17, that
was achieved by running the kernel function on 32 threads per block.
1
The Wireshark network protocol analyser ( ) was used
for this purpose.
2
118 Tests and conclusions
HtoD + Kernel + DtoH time [ms]
0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29 0.3
0
2
4
6
8
10
12
14
16
18
20
sum3
Entries 100
Mean 0.2708
RMS 0.005064
Total GPU trigger execution time
L0 cuts
0
π
+
π
64≤
hit
n≤ 5
-
π
+
π
+
π
(a) Total GPU trigger latency for a batch of 256 events
Batch number
0 10 20 30 40 50 60 70 80 90 100
CUDA total execution time [ms]
0.22
0.24
0.26
0.28
0.30
0.32
0.34
0.36
0.38
Time stability
Standard L0 cuts
0
π
+
π
64≤
hit
n≤ 5
0
π
+
π
Standard L0 cuts
-
π
+
π
+
π
64≤
hit
n≤ 5
-
π
+
π
+
π
Standard L0 cutsνν
+
π
64≤
hit
n≤ 5νν
+
π
(b) Total GPU latency as a function of the number of iterations.
Figure 8.4:
Total trigger execution time for 256 L0-filtered
π+π0
and 256 unfiltered
π+π+π−
events (top panel). The measurement was repeated 100 times. The bottom plot
shows the same quantity as a function of the number of iteration, and for all the data sets
used for the tests discussed in Section 8.1.

8.3 Possible improvements and outlook 119
The above reported timing tests are encouraging. In particular, from the
results in Eqns. 8.17 and 8.19 we learn that 10 Tesla K20-equivalent GPUs
would be enough to handle a data input rate of 10
MHz
. A “triggerless”
approach using normal processors would require a much more larger and
expensive PC farm.
8.3 Possible improvements and outlook
The algorithm developed for this thesis focusses on the suppression of
residual
K+→π+π0
background after the standard hardware L0 selection.
However, the results shown in the preceding sections suggest that such
an approach could allow to drop the hit multiplicity requirement from the
standard hardware L0 trigger.
A GPU trigger might therefore be optimized to this end, and it should
be investigated whether it could be used to suppress both the
π+π0
and
the
3π
backgrounds to the levels currently achieved by the standard trigger
(Table 3.2).
In particular, a more thorough Montecarlo study should support the
design of a
π+π+π−
rejection trigger. If the average ring multiplicity proves
to be sensibly higher than 2 for an important fraction of events, the idea of
creating more triplets should be considered. For example, after the defini-
tion of the initial , , and triplets, one could rotate the
PMTs frame by 45◦, and define 4 new triplets as before.
A dedicated Montecarlo simulation should be prepared in order to test
the ring identification efficiency in 3-ring and 4-ring events.
The time performance of the trigger might be further improved in many
ways. As a starting point, the framework should be tested with a continuous
stream of data (if the TEL62 boards could not be used for this purpose,
with controllable simulated data, a very large batch of data could be looped
between two Ethernet interfaces of the same PC). In this way one could
optimise the maximum number of events processed per batch ( ),
that was set to 256 in order not to increase the actual largest latency of the
process, i.e. the time elapsed while the host accumulates the data to process
on the GPU, that scales almost linearly with the number of events [42,55].
Moreover, alternative designs might be taken into consideration. In the

120 Tests and conclusions
Figure 8.5:
Using RICH and CHOD at the L1 trigger level, it would be possible to reduce
the rate of
π+π0
down to approximately 20%, even with a limited resolution on the
reconstruction of the decay vertex. Plot from [41].
present implementation of the algorithm, during the single-ring fit routine
only one thread executes the operations issued, except for the reduction of
the arrays. In particular, the function, listed in Appendix B, exploits
a Newton method to find the roots of the characteristic polynomial from
which the best ring parameters are later extracted. This part of the fitting
routine cannot be parallelized, and it might be moved to the host.
Another solution was proposed by G. Lamanna: we could exploit work-
load parallelization only at the event level, dropping the organization in
blocks and allocating a thread for each event. This way the code would
be serialized, and therefore easier to maintain; however, the number of
events processed per batch would be much larger, and tests should be done
to verify if the whole process – accumulation of data plus execution of the
trigger process – exhibits a latency low enough to be used as real-time trigger.
From the point of view of the selections that could be performed at the
first trigger levels, additional background rejection could be obtained at L1
by relating the information from the RICH to that of another detector able to
measure the position of the crossing track, like the CHOD. Figure 8.5 shows
that most of the residual
π+π0
content after the L0 selection is characterised
by a production vertex very close to the RICH detector, out of the fiducial
zv tx
region allowed for the signal analysis [41]. The angle information from
the RICH and the track impact point on the CHOD could be combined to
propagate the track backwards until it crosses the beam axis. This way, even
with a relatively poor longitudinal vertex resolution of
∼
10
m
, up to 80% of
the residual π+π0events could be rejected.

8.4 Conclusions 121
8.4 Conclusions
This research project represents the first approach to a GPU-based real-time
trigger solution in High Energy Physics experiments. It started as a bare idea,
supported by early tests by the NA62 collaboration [26,43,55], and that
idea has now been implemented into a working online trigger framework
prototype.
A fast, parallelized and seedless algorithm has been developed, capable
of finding multiple rings at real-time trigger level, a challenging idea that
proved to be feasible. The possibility to fit ˇ
Cerenkov rings online allows
selective trigger conditions to be set, based on kinematical constraints: the
radius and centre of the rings in fact provide a rough measurement of the
particle momentum and of its direction, with an assumption on the particle
type.
The analysis reported in Chapter 5demonstrates that the main back-
ground processes can be suppressed, by at least 60%, in addition to what
can be achieved by a non-selective hardware L0 trigger. Basic kinematical
analysis can be performed on data coming from a single detector in order
to provide early trigger decisions. If this idea is pursued, it could lead to a
“triggerless” design of future experiments: data could be evaluated in real
time in order to assess the signal and background content, with no need for
a previous event selection performed in hardware.
Within the scope of the NA62 experiment, a GPU-based trigger could
be built, that reduces the data rate arising from
π+π0
events up to 92%
for high PMT hit multiplicity events. The results reported in Section 8.1
demonstrate that also the
π+π+π−
background can be suppressed down to
a similar level, even with a non optimized algorithm. Additional trigger
requirements may be set up in order to further reduce this rate and to
increase the trigger rejection for low multiplicity events. Moreover, this
approach makes it possible to set up specific triggers for lepton number and
lepton flavour violating K+decay modes, as discussed in Section 6.1.
The latency of the GPU-based algorithm developed for this thesis proved
to be stable, and low enough to be compatible with the requirements of a
real-time trigger for high rate experiments.
The results reported in this thesis prove that alternative trigger designs
are feasible for the NA62 experiment, and dedicated triggers to study other

122 Tests and conclusions
K+decay modes are accessible and should be further investigated.
The graphics cards industry has seen lively development since the first
Personal Computers were released. Today, this sector is one of the most
supported by the IT industry. General-Purpose computing on GPUs is a new
research branch in fast expansion, that has already introduced advantages
for scientific computing.
This work represents a starting point to introduce the use of flexible
GPU-based real-time triggers in High Energy Physics.

A
Ring fitting algorithms
Contents
A.1 Problem definition ..................... 123
A.1.1 Geometrical parametrisation ............124
A.1.2 Algebraic parametrisation ..............125
A.2 The “math” algorithm ................... 126
A.2.1 Implementation of the “math” algorithm ......127
A.3 The Taubin algorithm ................... 129
A.3.1 Implementation of the Taubin algorithm ......131
A.1 Problem definition
Two approaches exist to the problem of fitting a circle to experimental data.
Our final purpose is to minimize the distance between our set of data points
(xi, yi)
and a generic circle, finding the parameters identifying the best fitting
ring. This can be achieved in one of two ways:
•iterative methods that converge to the minimum of
F=
i
d2
i(A.1)
di=(xi−a)2+ (yi−b)2−R(A.2)

124 Ring fitting algorithms
where the
di
are the
orthogonal
(geometric) distances from the ex-
perimental points
(xi, yi)
to the hypothetical circle of centre
(a, b)
and
radius R;
•
approximate algorithms that replace the distances with some other
quantities
fi
defined by simple algebraic rules, and minimize the
resulting sum
F=
i
f2
i(A.3)
These two types of fitting algorithms are referred to as
geometric
and
alge-
braic algorithms, respectively.
In the next sections I will briefly discuss the algorithms used for this
project. The
math
algorithm is the simplest mathematical approach to the
problem, whereas the
Taubin
method makes use of some approximation to
improve robustness and computational ease. They are both algebraic fitting
algorithms. Nevertheless, after the fitting, the circle must be expressed in
its geometrical parametrisation in order to extract the data we need, i.e.
the radius and the position of the centre. It will be convenient to start the
discussion from the two possible parametrisations, geometric and algebraic,
and the relationship between them.
A.1.1 Geometrical parametrisation
The canonical equation of a circle of centre (a, b)and radius Ris
(x−a)2+ (y−b)2−R2= 0 (A.4)
with the constraint
R > 0
. If we define
ri(a, b)≡(xi−a)2+ (yi−b)2
,
then the minimization function becomes
F(a, b, R) =
i
(ri−R)2(A.5)
and its minimum with respect to
R
is attained at
ˆ
R=1
niri= ¯r
, where
n
is the number of data points.
ˆ
R
is the best estimator for the radius
R
in this
picture. We can then express
F
as a function of the two variables
a
and
b
only:
F(a, b, ¯r) =
i
(ri−¯r)2(A.6)
=
i(xi−a)2+ (yi−b)2−1
n
j(xj−a)2+ (yj−b)22
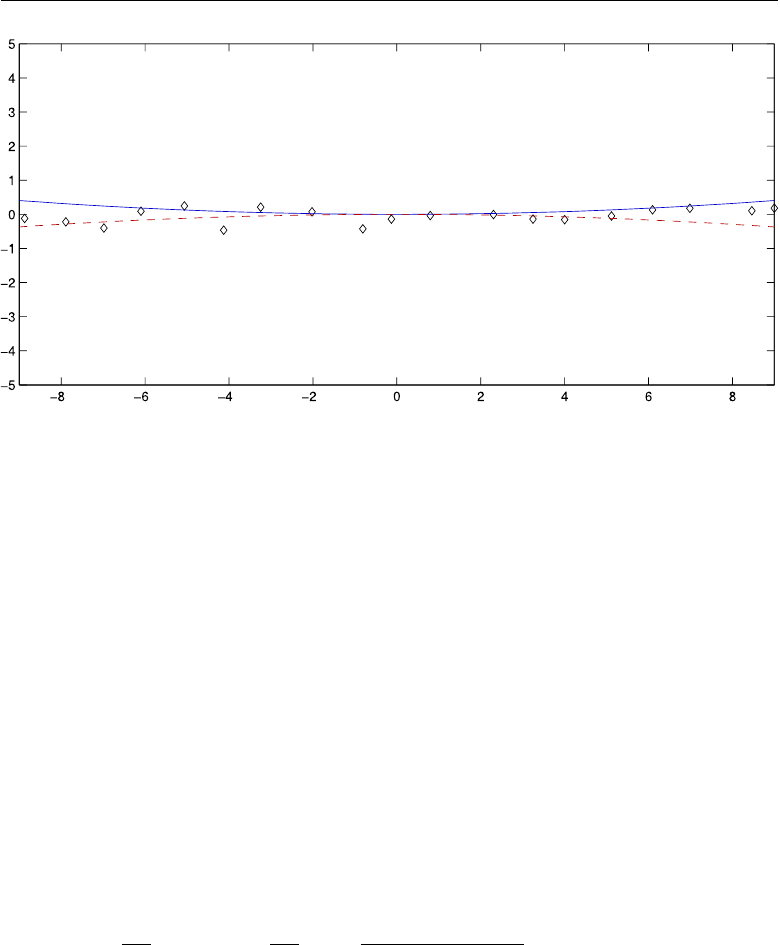
A.1 Problem definition 125
Figure A.1:
Data points sampled along a short arc. The blue line represents the correct fit.
A small inaccuracy may produce a wrong fit (dashed line) with opposite curvature [24].
A drawback of this parametrisation is that its robustness with respect
to the parameter
R
is poor when treating experimental points that lie on a
very short arc. A small perturbation may result in arbitrarily large values of
R, even with opposite signs (Figure A.1).
A.1.2 Algebraic parametrisation
An more elegant approach to the problem was proposed by Pratt in 1987
[56]. A circle is algebraically described by the equation
Ax2+y2+Bx +Cy +D= 0 (A.7)
or, equivalently,
x+B
2A2
+y+C
2A2
−B2+C2−4AD
4A2= 0 (A.8)
Compared to Eqn. A.7, Eqn. A.8 has the advantage of making two
constraints explicit:
A= 0 (A.9)
B2+C2−4AD > 0(A.10)
An additional constraint may be set, since the circle parameters only need
to be determined up to a multiplicative factor. Indeed, setting
A= 1
leads

126 Ring fitting algorithms
to the usual canonical equation A.4.
Pratt’s choice is more convenient: the choice of
B2+C2−4AD = 1 (A.11)
A > 0(A.12)
automatically ensures the constraint
B2+C2−4AD > 0
. The condition on
the sign of
A
ensures a unique correspondence between a set of parameters
(A, B, C, D)
and a circle. With this parametrisation, the distance of a point
(xi, yi)to the circle is given (after some algebraic manipulations) by
li=2Fi
1 + √1+4AFi
(A.13)
where
Fi=Ax2
i+y2
i+Bxi+Cyi+D(A.14)
1+4AFi=(xi−a)2+ (yi−b)2
R2(A.15)
The term
1+4AFi
inside the square root is always positive, hence
li
is always
computable. This formula can be proved to be more numerically robust as
compared to the geometric parametrisation [24].
Conversion formulas between algebraic and geometric parameters
a=−B
2Ab=−C
2AR2=B2+C2−4AD
4A2(A.16)
A=±1
2RB=−2Aa C =−2Ab D =B2+C2−1
4A(A.17)
Let us now see the two algorithms math and Taubin I mentioned at the
beginning of this chapter.
A.2 The “math” algorithm
Let us define
fi≡(xi−a)2+ (yi−b)2−R2(A.18)

A.2 The “math” algorithm 127
The simplest algebraic model to fit a circle
(xi−a)2+ (yi−b)2+R2= 0
to
a set of points would minimize the algebraic expression [19,24]
F1=
i
f2
i(A.19)
Note that
fi
does not represent the square orthogonal distance to the circle
of the point
(xi, yi)
defined in Eqn. A.2. However,
fi
is small if and only if
the point lies near to the circle: for this reason, some authors [56] call
fi
the algebraic distance from
(xi, yi)
to the circle. This approach is also the
base for the Kåsa, Pratt, and Taubin algorithms.
The change of parameters described in Eqns. A.16 and A.17 with the
choice A≡1linearises the derivatives of the objective function F1:
F1=
ix2
i+y2
i+Bxi+Cyi+D2(A.20)
Now differentiating
F1
with respect to the parameters
B, C, D
yields a
system of linear equations, by solving which we can compute
B, C, D
and,
finally, convert them back to the geometrical parameters a, b, R [24].
A.2.1 Implementation of the “math” algorithm
We will solve the problem in a suitable
(u, v)
coordinate system, and then
transform the solutions back to the laboratory frame (x, y)[19]. Writing
¯x=1
n
i
xi¯y=1
n
i
yi(A.21)
ui≡xi−¯x vi≡yi−¯y(A.22)
we obtain:
F1=
i
g2
i(A.23)
gi= (ui−uc)2+ (vi−vc)2−R2(A.24)
where
(uc, vc)
are the coordinates of the centre of the circle, as computed in
the (u, v)frame:
uc=a−¯x(A.25)
vc=b−¯y(A.26)

128 Ring fitting algorithms
In order to minimize
F1
we compute its derivatives with respect to the
parameters uc,vcand R2:
∂F1
∂R2= 2
i
gi
∂gi
∂R2=−2
i
gi(A.27)
∂F1
∂uc
= 2
i
gi
∂gi
∂uc
=−4
i
uigi+ 4uc
i
gi(A.28)
∂F1
∂vc
= 2
i
gi
∂gi
∂vc
=−4
i
vigi+ 4uc
i
gi(A.29)
and then set them to zero. This system gives the unique solution
i
gi= 0
i
uigi= 0
i
vigi= 0 (A.30)
Now let
Su≡
i
uiSuu ≡
i
u2
iSuuu ≡
i
u3
ietc. (A.31)
and similarly for
Sv, Suv
and so on, where
Su=Sv= 0
by definition.
Adopting this notation, if we expand Eqns. A.30 we obtain the system
ucSuu +vcSuv =1
2(Suuu +Suvv)(A.32)
ucSuv +vcSvv =1
2(Svvv +Suuv)(A.33)
nu2
c+v2
c−R2+Suu +Svv = 0 (A.34)
which in turn yelds the solutions
uc=
Suv
2(Svvv +Suuv)−Svv
2(Suuu +Suvv)
S2
uv −S2
v v
(A.35)
vc=
1
2(Suuu +Suvv)−ucSuu
Suv
(A.36)
R2=u2
c+v2
c+Suu +Sv v
n(A.37)
The centre of the circle in the original coordinate system will be
(a, b) =
(uc, vc) + (¯x, ¯y).

A.3 The Taubin algorithm 129
A.3 The Taubin algorithm
The very simple ring fitting algorithm developed by Kåsa and the later, more
stable and “elegant” Pratt modification are throughly described in [24,56,
66] and we will not discuss them here in detail.
Another method for algebraic circle fitting was proposed in 1991 by
Gabriel Taubin [66]. His method is very similar to the Pratt algorithm both
in design and performance, but:
•it can be generalized to ellipses and other algebraic curves;
•it features smaller bias and higher statistical accuracy;
•it requires simpler computations, and therefore it is less “expensive”.
The Taubin algorithm is based on the minimization of the function
F2=i(xi−a)2+ (yi−b)2−R22
i(xi−a)2+ (yi−b)2(A.38)
as a result of the development of few simple algebraic ideas.
Take the so-called algebraic distances
fi
as defined in Eqn. A.18. Now
consider the expansion
ri≡(xi−a)2+ (yi−b)2(A.39)
fi= (ri−R)(ri+R)(A.40)
The Kåsa and “math” methods effectively minimize the sum F1=id2
iD2
i,
where we can identify the two factors as the distances from the
i−
th point to
the nearest point of the circle (
di=ri−R
, as defined in Eqn. A.2) and to the
farthest point on the circle (
Di=ri+R
). Unfortunately, this is the reason
why the Kåsa method, and therefore also the “math” mathod, are heavily
biased towards smaller circles, underestimating the radius when the data
points lie on a short arc. By minimizing the averaged product of
d2
i
and
D2
i
one may only find the best trade-off between the two distances: a smaller
circle would yeld smaller
D2
i
, minimizing
F1
regardless of the larger
d2
i
[24].
The solution found by Pratt [56] solves the statistical bias introduced by
Kåsa, but involves matrix algebra and therefore it is less numerically stable.
Now observe that, if the points are close to the circle,
Di=di+ 2R
|di| R=⇒ F1≈4R2
i
d2
i(A.41)

130 Ring fitting algorithms
A natural assumption |di| Ryields:
R2≈(R+di)2= (xi−a)2+ (yi−b)2=r2
i(A.42)
Positive and negative fluctuations will tend to cancel out if we average over
the whole sample:
R2≈1
n
i(xi−a)2+ (yi−b)2=1
n
i
r2
i(A.43)
Eqn. A.41 now factorizes into
F1≈4
n
i
r2
i×
i
d2
i≡ Fr× Fd(A.44)
We ultimately wish to minimize the second factor (
Fd
). Comparing Eqns. A.18–
A.19 and the expression A.41 for
F1
, we can define a new minimization
function F2≡ F1/Fr
F2=i(xi−a)2+ (yi−b)2−R22
4/n i(xi−a)2+ (yi−b)2
=i(zi−2axi−2byi+a2+b2−R2)2
4/n i(zi−2axi−2byi+a2+b2)(A.45)
by minimizing which we can approximately achieve our goal. Above, we
denoted zi≡x2
i+y2
ifor brevity.
Switching to the algebraic parameters
(A, B, C, D)
defined in Eqn. A.17,
we get
F2=ni(Azi+Bxi+Cyi+D)2
i(4A2zi+ 4ABxi+ 4ACyi+B2+C2)(A.46)
The minimization of A.46 is equivalent to minimizing
F3≡
i
(Azi+Bxi+Cyi+D)2(A.47)
with respect to the parameters (A, B, C, D), with the constraint
4A2zi+ 4ABxi+ 4ACyi+B2+C2= 1 (A.48)
as discussed in Section A.1.2.

A.3 The Taubin algorithm 131
Finally, in
matrix form
, Taubin’s algorithm requires the minimization of
F3(A) = ATXTXA(A.49)
with the constraint ATTA = 1, where:
A=
A
B
C
D
T=
4z2x2y0
2x1 0 0
2y0 1 0
0 0 0 0
(A.50)
X=
z1x1y11
.
.
..
.
..
.
..
.
.
znxnyn1
(A.51)
where ¯z=1
nizi, and Xis called the extended data matrix.
A.3.1 Implementation of the Taubin algorithm
Eqns. A.46,A.47 and A.48 can be much simplified, reducing the problem to
that of finding the roots of a third order polynomial [24].
F2
is a second order polynomial in
D
, and therefore admits a unique
minimum in
D=−Az −Bx −Cy
. Substituting in Eqn. A.48, we get the
equations of the two constraints to the minimization of F2(Eqn. A.47):
D=−Az −Bx −Cy (A.52)
B2+C2−4AD = 1 (A.53)
Now perform the change of coordinates described in Eqn. A.22, and let
wi≡u2
i+v2
i. The above contraints become
D=−Aw (A.54)
A2
0+B2+C2= 1 (A.55)
having defined
A2
0≡4wA2
, and the function to minimize can be written as
F5=
iwi−w
2√wA0+Bui+Cvi2
(A.56)
In matrix form, this corresponds to
F5(A0) = A0TUTUA0
A0TA0= 1 (A.57)

132 Ring fitting algorithms
where
A0=
A0
B
C
U=
(w1−w)/2√w u1v1
.
.
..
.
..
.
.
(wn−w)/2√w unvn
(A.58)
are the modified vector of parameters and data matrix.
The minimization can be performed using a Lagrange multiplier η:
G(A0, η)≡A0TUTUA0−ηA0TA0−1(A.59)
∂G
∂A0
=UTUA0−ηA0≡0(A.60)
UTUA0=ηA0(A.61)
Our algorithm reduces to the
eigenvalue problem
of Eqn. A.61. Observe
that
F5(A0) = A0TUTUA0=ηA0TA0=η(A.62)
The minimum of Eqn. A.56 is therefore attained by the eigenvector
A0
of
UTU
corresponding to its smallest eigenvalue
η
[24].
UTU
is symmetric
and positive-definite, therefore its eigenvalues are all real and positive. The
characteristic equation of this problem
det ηI−UTU= 0 (A.63)
can be written as a third order polynomial in η:
p(η) = c0+c1η+c2η2+c3η3= 0 (A.64)
with
c0=uw (uw v2−vw uv)
+vw (vw x2−uw uv)−Var zCov(x, y)(A.65)
c1= [Var z+ 4Cov(x, y)] w−uw2−vw2(A.66)
c2=−3w2−w2(A.67)
c3= 4w(A.68)
Var z=w2−w2(A.69)
Cov(x, y) = u2v2−uv2(A.70)
Observing the coefficients and the form of p(η), we find that:

A.3 The Taubin algorithm 133
•p(η= 0) = det −UTU<0
(the matrix results singular only in the
case that all the experimental points lie exactly on a circle).
•p(η= 0) <0
, and the only root of
p(η) = 0
is
η2=−2c2/6c3>0
.
Hence, p(η)<0in the interval between 0and its lowest root.
The latter point implies that the function
p(η)
is convex upwards. Therefore
a
Newton
procedure supplied with the initial guess
η= 0
is bound to con-
verge to the smallest positive root of p(η)[24].
Once the eigenvalue
η
is computed, the circle parameters can be found
simply solving the equation for the corresponding eigenvector A
0:
UTU−ηIA
0= 0 (A.71)

B
CUDA code for the Taubin algorithm

136 CUDA code for the Taubin algorithm

137

C
Specifications of the NVIDIA Tesla K20 GPU
Device 0: "Tesla K20c"
CUDA Driver Version / Runtime Version 5.0 / 5.0
CUDA Capability Major/Minor version number: 3.5
Total amount of global memory: 4800 MBytes (5032706048 bytes)
(13) Multiprocessors x (192) CUDA Cores/MP: 2496 CUDA Cores
GPU Clock rate: 706 MHz (0.71 GHz)
Memory Clock rate: 2600 Mhz
Memory Bus Width: 320-bit
L2 Cache Size: 1310720 bytes
Total amount of constant memory: 65536 bytes
Total amount of shared memory per block: 49152 bytes
Total number of registers available per block: 65536
Warp size: 32
Maximum number of threads per multiprocessor: 2048
Maximum number of threads per block: 1024
Maximum sizes of each dimension of a block: 1024 x 1024 x 64
Maximum sizes of each dimension of a grid: 2147483647 x 65535 x 65535
Maximum memory pitch: 2147483647 bytes
Texture alignment: 512 bytes
Concurrent copy and kernel execution: Yes with 2 copy engine(s)
Run time limit on kernels: No
Integrated GPU sharing Host Memory: No
Support host page-locked memory mapping: Yes
Alignment requirement for Surfaces: Yes
Device has ECC support: Enabled
Device supports Unified Addressing (UVA): Yes
Device PCI Bus ID / PCI location ID: 132 / 0
Table C.1:
Technical characteristics of the GPU on which this project was implemented
and tested. Data obtained by means of the script provided with the CUDA
libraries ( ).

Bibliography
[1]
R. AAIJ et al. Measurement of the
B0
s−¯
B0
s
oscillation frequency
∆ms
in
B0
s→D−
s(3)π
decays. Phys. Lett. B 709 (2012), pp. 177–184. DOI:
.
[2]
A. ABULENCIA et al. Observation of B0(s) - anti-B0(s) Oscillations.
Phys. Rev. Lett. 97 (2006). DOI: .
[3]
K. AHMET et al. The OPAL detector at LEP. Nucl. Instrum. Meth. A
305 (1991), pp. 275–319. DO I: .
[4]
D. AMBROSE et al. New limit on muon and electron lepton number vi-
olation from
K0
L→µ±e∓
decay. Phys. Rev. Lett. 81 (1998), pp. 5734–
5737. DOI: .
[5]
B. ANGELUCCI et al. TEL62: an integrated trigger and data acquisition
board. Journal of Instrumentation 7.02 (2012). DOI:
.
[6]
B. AN GELUCCI. “Trigger simulation update”. NA62 Physics WG meet-
ing. Aug. 2013.
[7]
V. V. ANISIMOVSKY et al. Improved measurement of the
K→πν ¯ν
branching ratio. Phys. Rev. Lett. 93 (2004), p. 031801. DOI:
.
[8]
G. ANZIVINO et al. Construction and test of a RICH prototype for the
NA62 experiment. Nucl. Instrum. Meth. A 593 (Aug. 2008), pp. 314–
318. DOI: .

142 BIBLIOGRAPHY
[9]
A. V. ARTAMONOV et al. New measurement of the
K+→π+ν¯ν
branching ratio. Phys. Rev. Lett. 101 (2008), p. 191802. DOI:
.
[10]
A. V. ARTAMONOV et al. Study of the decay
K+→π+ν¯ν
in the
momentum region
140 < Pπ<199 MeV/c
.Phys. Rev. D 79 (9 May
2009). DOI: .
[11]
Y. ASANO et al. Search for a rare decay mode
K→πν ¯ν
and axion.
Physics Letters B 107.1-2 (Dec. 1981), pp. 159–162. DOI:
.
[12]
H. W. ATHERTON et al. Precise measurements of particle production by
400 GeV/c protons on beryllium targets. Geneva: CERN, 1980.
[13]
G. ATOIAN et al. Lead scintillator electromagnetic calorimeter with
wavelength shifting fiber readout. Nucl. Instrum. Meth. A 320 (1992),
pp. 144–154. DO I: .
[14]
J. BATLEY et al. New measurement of the
K±→π±µ+µ−
decay. Phys.
Lett. B 697 (2011), pp. 107–115. DOI:
.
[15]
N. BERGER. Partial wave analysis at BES III harnessing the power
of GPUs. American Institute of Physics Conference Series 1374 (Oct.
2011). Ed. by D. ARMSTRONG et al., pp. 553–556. DOI:
.
[16]
J. BROD, M. GORBAHN and E. STAMOU. Two-loop electroweak cor-
rections for the
K→πνν
decays. Phys. Rev. D 83 (3 Feb. 2011). DOI:
.
[17]
G. BUCHALLA and A. J. BURAS. QCD corrections to the anti-s d Z
vertex for arbitrary top quark mass. Nucl. Phys. B 398 (1993), pp. 285–
300. DOI: .
[18]
G. BUCHALLA and A. J. BURAS. The rare decays
K→πν¯ν
and
KL→µ+µ−
beyond leading logarithms. Nucl. Phys. B 412 (1994),
pp. 106–142. DO I: .
[19]
R. BU LLOCK .Least-Squares Circle Fit. Developmental Testbed Center.
2006.
[20]
N. CABIBBO. Unitary Symmetry and Leptonic Decays. Phys. Rev. Lett.
10 (12 1963), pp. 531–533. DO I: .
[21]
G. D. CABLE et al. Search for Rare
K+
Decays. II.
K+→π+ν¯ν
.Phys.
Rev. D 8 (11 Dec. 1973), pp. 3807–3812. DOI:
.

BIBLIOGRAPHY 143
[22]
U. CAMERINI et al. Experimental Search for Semileptonic Neutrino
Neutral Currents. Phys. Rev. Lett. 23 (6 Aug. 1969), pp. 326–329. DOI:
.
[23]
A. CECCUCCI.NA62/P-326 Status Report. Tech. rep. SPS Experiments
Committee, CERN, Nov. 2007.
[24]
N. CHERNOV.Circular and linear regression: Fitting circles and lines by
least squares. Chapman & Hall/CRC, 2010. IS BN: 1439835906.
[25]
G. COLLAZUOL et al. “Fast FPGA-based Trigger and Data Acquisition
System for the CERN Experiment NA62: Architecture and Algorithms”.
In: 11th EUROMICRO Conference on Digital System Design Architec-
tures, Methods and Tools. 2008, pp. 405–412. DO I:
.
[26]
G. COLLAZUOL et al. Fast online triggering in high-energy physics
experiments using GPUs. Nucl. Instrum. Meth. A 662 (2012), pp. 49–
54. DOI: .
[27]
H. S. M. COXETER and S. L. GREITZER.Geometry Revisited. The
Mathematical Association of America, 1967. IS BN: 0883856190.
[28]
FLAVIANET MARIE CURIE TRAINING NETWORK.Working Group on
Precise SM Tests in K Decays. June 2010. URL:
.
[29]
J. M. FLYNN, M. PAULINI and S. WILLOCQ .WG2 Conveners’ Report:
Vtd and Vts, B-Bbar mixing, radiative penguin and rare (semi)leptonic
decays. Tech. rep. Nov. 2003. arXiv: .
[30]
S. GORBUNOV et al. ALICE HLT High Speed Tracking on GPU. IEEE
Transactions on Nuclear Science 58.4 (2011), pp. 1845–1851. DOI:
.
[31]
G. HAEFELI et al. The LHCb DAQ interface board TELL1. Nucl. Instrum.
Meth. A 560 (2006), pp. 494–502. DOI:
.
[32]
F HAHN et al. NA62: Technical Design Document. Tech. rep. NA62-10-
07. Geneva: CERN, Dec. 2010.
[33]
M. J. HARRIS. “Optimizing Parallel Reduction in CUDA”. NVIDIA
Developer Technology. URL:
.
[34]
M. J. HARRIS.Real-Time Cloud Simulation and Rendering. PhD thesis.
Department of Computer Science, University of North Carolina at
Chapel Hill, 2003. UR L: .

144 BIBLIOGRAPHY
[35]
T. HURTH et al. Constraints on New Physics in MFV models: A Model-
independent analysis of
∆
F = 1 processes. Nucl. Phys. B 808 (2009),
pp. 326–346. DO I: .
[36]
G. ISIDORI, F. MESCIA and C. SMITH. Light-quark loops in
K→πν¯ν
.
Nucl. Phys. B 718 (2005), pp. 319–338. DOI :
.
[37]
E. IWAI. Status and prospects of J-PARC KOTO experiment. Nucl. Phys.
Proc. Suppl. 233 (2012), pp. 279–283. DOI:
.
[38]
D. E. JAFFE and S. YOUSS EF. Bayesian estimate of the effect of
B0¯
B0
mixing measurements on the CKM matrix elements. Comput. Phys.
Commun. 101 (1997), p. 206. DOI:
.
[39]
M. KOBAYASHI and T. MASKAWA. CP Violation in the Renormalizable
Theory of Weak Interaction. Prog. Theor. Phys. 49 (1973), pp. 652–
657. DOI: .
[40]
J. LAIHO, E. LUNGHI and R. S. VAN DE WATER . Lattice QCD inputs
to the CKM unitarity triangle analysis. Phys. Rev. D 81 (2010). DOI:
.URL:
.
[41]
G. LAMANNA. “2 rings trackless fitting for L1/L0 RICH trigger using
GPU”. NA62 Trigger and Data Acquisition WG meeting. May 2011.
[42]
G. LAMANNA. “GPU for realtime processing in HEP experiments”.
In: EPS-HEP 2013, Stockholm.URL:
.
[43]
G. LAMANNA. “GPUs for fast triggering in NA62 experiment”. In:
Technology and Instrumentation in Particle Physics. June 2011. URL:
.
[44]
I. MANNELLI. “NEWCHOD: Preliminary construction ideas”. NA62
joint MUV/CHOD WG meeting. June 2013.
[45]
H. MCKENDRICK.Analysis Acceleration in TMVA for the ATLAS Experi-
ment at CERN using GPU Computing. PhD thesis. School of Informatics,
University of Edinburgh, 2011.
[46]
F. MESCIA and C. SMITH. Improved estimates of rare K decay matrix-
elements from Kl3 decays. Phys. Rev. D 76 (2007). DOI:
.

BIBLIOGRAPHY 145
[47]
M. MISIAK and J. URBAN. QCD corrections to FCNC decays mediated
by Z penguins and W boxes. Phys. Lett. B 451 (1999), pp. 161–169.
DOI: .
[48]
NA48 COLLABORATION et al. The beam and detector for the NA48
neutral kaon CP violation experiment at CERN. Nucl. Instrum. Meth. A
574 (May 2007), pp. 433–471. DO I: .
[49]
NA62 COLLABORATION.2013 NA62 Status Report to the CERN SPSC.
Tech. rep. SPS and PS Experiments Committee, CERN, Mar. 2013.
[50]
K. NAKAMURA et al. Review of Particle Physics. Journal of Physics G:
Nuclear and Particle Physics 37.7A (2010). URL: .
[51]
F. O. NEWSON. “Kaon experiments at CERN: recent results and
prospects”. In: PSI 2013. 2013. URL:
.
[52]
M. NICULESCU and S.-I. ZGURA. Computing trends using graphic pro-
cessor in high energy physics. ArXiv e-prints (June 2011). arXiv:
.
[53]
NVIDIA CORPORATION.NVIDIA CUDA C Programming Guide. July
2013. URL: .
[54]
F. PANTALEO et al. “Real-Time Use of GPUs in NA62 Experiment”. In:
13th International Workshop on Cellular Nanoscale Networks and their
Applications. Geneva, Aug. 2012.
[55]
F. PANTALEO et al. “Real-time triggering in HEP using GPUs”. In:
GPU Technology Conference. Mar. 2013. UR L:
.
[56]
V. PRATT. Direct least-squares fitting of algebraic surfaces. SIGGRAPH
Comput. Graph. 21.4 (Aug. 1987), pp. 145–152. DOI:
.
[57]
S. RENNIC H. “CUDA C/C++ Streams and Concurrency”. GPU Com-
puting webinars, NVIDIA Corp. URL:
.
[58]
A. ROMANO.Leptonic decays and Kaon identification at the NA62
experiment at CERN. PhD thesis. School of Physics and Astronomy,
University of Birmingham, Dec. 2012.
[59]
A. SERGI.Recent results from Kaon Physics. Tech. rep. Mar. 2013.
arXiv: .
[60]
A. SHER et al. An Improved upper limit on the decay
K+→π+µ+e−
.
Phys. Rev. D 72 (2005). DOI: .

146 BIBLIOGRAPHY
[61]
K. SHUM.Distance distribution in the hexagonal packing. Dec. 2012.
URL: .
[62]
M. SOZZ I. “A concept for the NA62 trigger and data acquisition”.
NA62 Internal Note. Nov. 2007.
[63]
M. SOZZI et al. “NA62 online software and TDAQ interface”. NA62
Internal Note. Feb. 2011.
[64]
M. STEIN. “CUDA Basics”. ManyCores Reading Group, New York
University. URL: .
[65]
S. TARIQ. “An Introduction to GPU Computing and CUDA Architec-
ture”. GPU Computing webinars, NVIDIA Corp. 2011. UR L:
.
[66]
G. TAUBIN. Estimation of Planar Curves, Surfaces, and Nonplanar
Space Curves Defined by Implicit Equations with Applications to
Edge and Range Image Segmentation. IEEE Trans. Pattern Anal. Mach.
Intell. 13.11 (1991), pp. 1115–1138. URL:
.
[67]
G. UNAL. “Performances of the NA48 Liquid Krypton Calorimeter”.
In: CALOR2000, Annecy. 2000. URL:
.
[68]
B. VELGHE. “GigaTracker, a Thin and Fast Silicon Pixels Tracker”.
In: RD13 - 11th International Conference on Large Scale Applications
and Radiation Hardness of Semiconductor Detectors. July 2013. URL:
.
[69]
J. VERSCHELDE. “Concurrent Kernels & Multiple GPUs”. Graduate
seminar lecture notes. University of Illinois, Chicago. Apr. 2012. URL:
.
[70]
A. WASHBROOK. “Algorithm Acceleration from GPGPUs for the ATLAS
Upgrade”. In: Conference on Computing in High Energy and Nuclear
Physics. Oct. 2010. UR L: .
[71]
L. WOLFENSTEIN. Parametrization of the Kobayashi-Maskawa Matrix.
Phys. Rev. Lett. 51 (21 Nov. 1983), pp. 1945–1947. DOI:
.

Acknowledgements
I would like to express my gratitude to my supervisor, who has always
been available and attentive, and has patiently guided and encouraged
me through the steps of my work with many enlightening advices and a
maddening attention to spelling and punctuation.
I thank Gianluca Lamanna, whose «Would it be easy to try this?...»
suggestions I learned to expect and to treasure (and they will probably
never stop until the very day of my graduation!).
Thanks to Felice, for his valuable help and company during the long
afternoons we spent writing and erasing code in front of the lab PCs.
Thanks to Roberto, Bruno and Jacopo for having always been willing
to help me during these long months. My deepest gratitude goes to all of
them.
I cannot keep myself from thanking all of my friends. I know that every
one of them will bring to themselves and to the people around them the
same enjoyable happiness that they have often brought to me.
Thanks to Martina, Alberto, Luigi, Daniele, Leslie, Massimo, Elena, Paola,
Marco, Sara, Andrea, Giovanni, Paola, Francesco, and to my dear flatmates
Cinzia, Eliana and Irene. I hope my fellow students did not mind that I
haunted our department as a thesis-writing ghost all the time. A special
mention to Francesco and Luca, my fellow coffee-seeking ghosts!
A heartfelt thought goes to Arianna: our paths split as we left Siena for
new adventures, but I know my friend will always be there when I need her.
I take this opportunity to express my profound gratitude to my family,
and especially to my parents, that have been a constant source of support
during my university years. It is to them that this thesis is dedicated.
Last but not least, my deepest gratitude goes to Salvo. Without his loving
support, it would have been much more difficult for me to go through these
challenging and sometimes stressful times.

